Capítulo 12 Variáveis qualitativa e quantitativa

12.1 Abordagem paramétrica

12.1.1 Teste t de Student para duas amostras

O Teste t de Student compara duas médias e mostra se as diferenças entre essas médias são significativas. Este teste permite que você avalie se a diferença entre duas médias ocorreram por acaso ou não. Este teste deve ser utilizado somente após a avaliação dos pressupostos de Normalidade, de homogeneidade de variâncias (variâncias iguais), e independência. Ele e realizado com a função t.test.

Utiliza-se este teste quando:
* Os dados seguem a Distribuição normal;
* Temos dois grupos;
* Concluimos no teste de Bartlett que os dois grupos têm variâncias iguais.

12.1.1.1 Dados apropriados

• A variável dependente é quantitativa.
• A variável independente é qualitativa com dois níveis.

12.1.1.2 Hipóteses

Hipótese nula: \[ \mu_1 = \mu_2 \]
Hipótese alternativa: \[ \mu_1 \neq \mu_2 \]

12.1.1.3 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa entre as médias dos dois grupos”.

12.1.1.4 Exemplo do teste t de Student

Este exemplo apresenta os dados de uma amostra de 32 carros.
Esse teste responde à pergunta: “A média da variável Km/L (quantitativa) é igual para os dois grupos de carros (gasolina/álcool)?”

#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
                      "Amperagem_circ_eletrico","Peso","RPM",
                      "Tipodecombustivel","TipodeMarcha",
                      "NumdeMarchas","NumdeValvulas")
CARROS$Tipodecombustivel<-as.factor(CARROS$Tipodecombustivel)
levels(CARROS$Tipodecombustivel) <- c('Gasolina','Álcool')

### Verifique os dados
str(CARROS$Kmporlitro)

##  num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...

str(CARROS$Tipodecombustivel)

##  Factor w/ 2 levels "Gasolina","Álcool": 1 1 2 2 1 2 1 2 2 2 ...

### Remova objetos desnecessários
remove(mtcars)

#### Resumo dos dados 
library(psych)
describeBy(CARROS$Kmporlitro,group = CARROS$Tipodecombustivel)

## 
##  Descriptive statistics by group 
## group: Gasolina
##    vars  n  mean   sd median trimmed  mad  min max range skew kurtosis   se
## X1    1 18 16.62 3.86  15.65   16.42 2.97 10.4  26  15.6 0.48    -0.05 0.91
## ------------------------------------------------------------ 
## group: Álcool
##    vars  n  mean   sd median trimmed mad  min  max range skew kurtosis   se
## X1    1 14 24.56 5.38   22.8   24.34   6 17.8 33.9  16.1 0.41     -1.4 1.44

#### Box-plot
boxplot(CARROS$Kmporlitro~CARROS$Tipodecombustivel,
        horizontal = TRUE,col=c("skyblue","red"))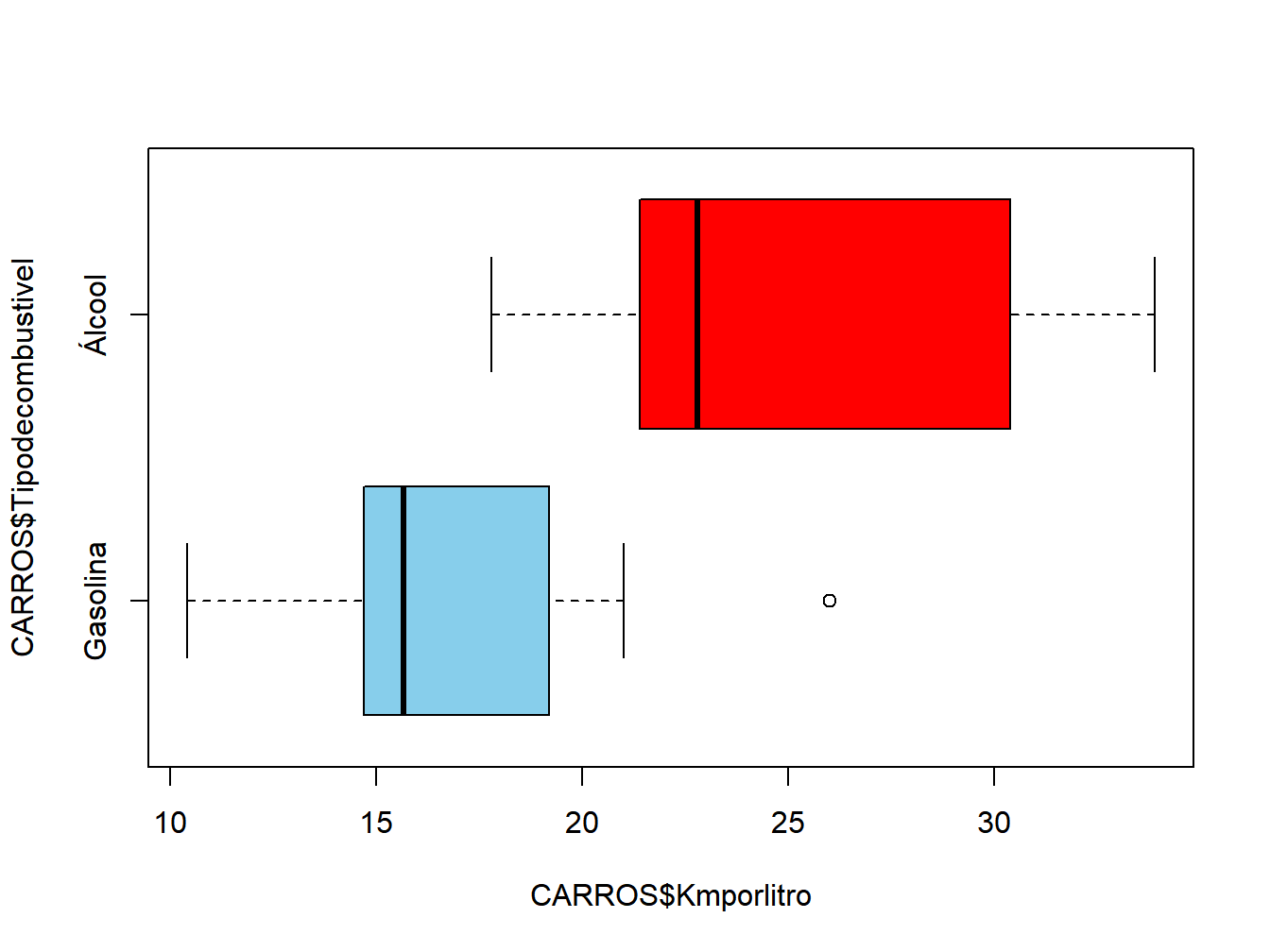

Figura 12.1: Teste de Shapiro Wilk

#### Teste t de Student 
t.test(CARROS$Kmporlitro~CARROS$Tipodecombustivel, var.equal=TRUE)

## 
##  Two Sample t-test
## 
## data:  CARROS$Kmporlitro by CARROS$Tipodecombustivel
## t = -4.8644, df = 30, p-value = 0.00003416
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -11.274221  -4.606732
## sample estimates:
## mean in group Gasolina   mean in group Álcool 
##               16.61667               24.55714

12.1.1.5 Teste t pareado

O teste t pareado é utilizado com amostras dependentes(pareadas). Em amostras pareadas para cada observação realizamos duas mensurações. As medidas são tomadas em um único indivíduo em dois pontos distintos no tempo. Em geral, observações pareadas correspondem a medidas tomadas antes e depois de uma intervenção.

Veja o exemplo a seguir, no qual existem um grupo de pacientes que teve alguma medida realizada antes da intervenção e outra depois da intervenção. Por exemplo, uma métrica de popularidade de políticos (de 0 a 100) antes e depois de uma campanha de marketing uma medida em uma comunidade antes e depois de uma política pública. O importante aqui é entendermos que as duas medidas são realizadas num mesmo grupo de pessoas, antes e depois de uma intervenção.

O teste t para amostras indepententes não exige que os grupos tenham o mesmo tamanho, mas observe que o teste t pareado exige que existam exatamente o mesmo número de medidas antes e depois. Para usar o teste t pareado, iremos simplesmente alterar o argumento paired:

#-------------------------------------------------------------
### Banco de dados
antes  <- c(21, 28, 24, 23, 23, 19, 28, 20, 22, 20, 26, 26)
depois <- c(26, 27, 23, 25, 25, 29, 30, 31, 36, 23, 32, 22)
dados<-data.frame(antes,depois)

## Grafico simples da diferenca
Diferenca <- (dados$depois - dados$antes)
plot(Diferenca,pch = 16,ylab="Diferença (Depois/antes)")
abline(0,0, col="blue", lwd=2)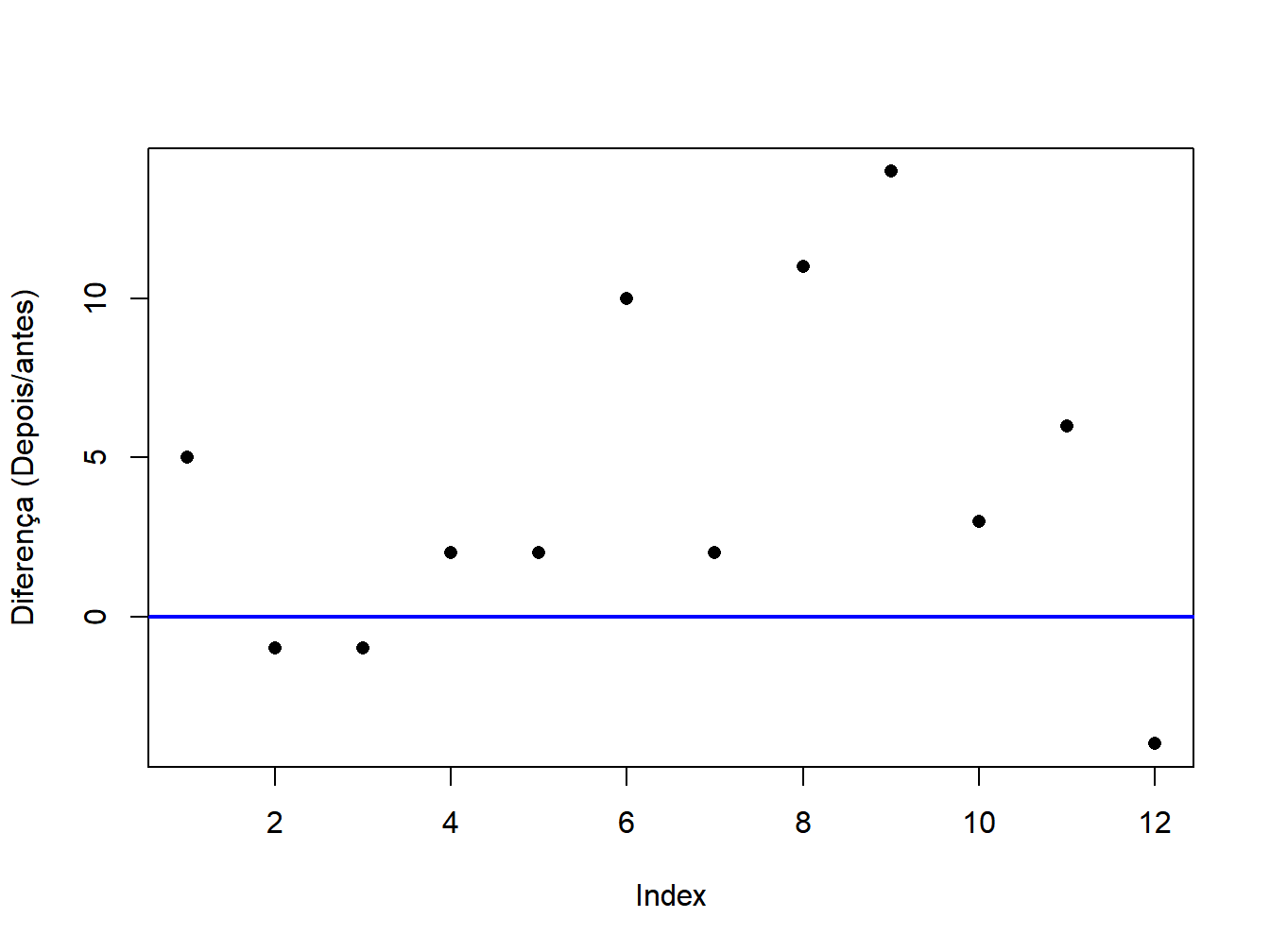

Figura 12.2: Teste

#### Teste t pareado
t.test(dados$antes, dados$depois, paired = TRUE)

## 
##  Paired t-test
## 
## data:  dados$antes and dados$depois
## t = -2.6353, df = 11, p-value = 0.02319
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -7.493713 -0.672954
## sample estimates:
## mean of the differences 
##               -4.083333

12.1.1.6 Interpretação do resultado do teste-t pareado

O teste é interpretado da mesma forma que o teste t para duas amostras independentes.

12.1.2 Teste-t de Welch de duas amostras (Teste t de Student com variâncias desiguais)

O teste-t de Welch compara duas médias e mostra se as diferenças entre essas médias são significativas. O teste-t de Welch é uma adaptação do teste t de Student, que é mais confiável quando as duas amostras têm variâncias desiguais.

Em outras palavras, este teste permite que você avalie se a diferença entre duas médias ocorreram por um mero por acaso ou não. Este teste deve ser utilizado somente após a avaliação do pressuposto de homogeneidade de variâncias (variâncias iguais).

Utiliza-se este teste quando:
* Os dados seguem a Distribuição normal;
* Temos dois grupos;
* Concluimos no teste de Bartlett que os dois grupos têm variâncias diferentes.

É realizado com a função t.test.

12.1.2.1 Dados apropriados

• A variável dependente é quantitativa.
• A variável independente é qualitativa com dois níveis.

12.1.2.2 Hipóteses

Hipótese nula: \[ \mu_1 = \mu_2 \] Hipótese alternativa: \[ \mu_1 \neq \mu_2 \]

12.1.2.3 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa entre as médias dos dois grupos”.

#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
                      "Amperagem_circ_eletrico","Peso","RPM",
                      "Tipodecombustivel","TipodeMarcha",
                      "NumdeMarchas","NumdeValvulas")
CARROS$Tipodecombustivel<-as.factor(CARROS$Tipodecombustivel)
levels(CARROS$Tipodecombustivel) <- c('Gasolina','Álcool')

### Verifique os dados
str(CARROS$Kmporlitro)

##  num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...

str(CARROS$Tipodecombustivel)

##  Factor w/ 2 levels "Gasolina","Álcool": 1 1 2 2 1 2 1 2 2 2 ...

### Remova objetos desnecessários
remove(mtcars)

#### Resumo dos dados 
library(psych)
describeBy(CARROS$Kmporlitro,group = CARROS$Tipodecombustivel)

## 
##  Descriptive statistics by group 
## group: Gasolina
##    vars  n  mean   sd median trimmed  mad  min max range skew kurtosis   se
## X1    1 18 16.62 3.86  15.65   16.42 2.97 10.4  26  15.6 0.48    -0.05 0.91
## ------------------------------------------------------------ 
## group: Álcool
##    vars  n  mean   sd median trimmed mad  min  max range skew kurtosis   se
## X1    1 14 24.56 5.38   22.8   24.34   6 17.8 33.9  16.1 0.41     -1.4 1.44

#### Box-plot
boxplot(CARROS$Kmporlitro~CARROS$Tipodecombustivel,
        horizontal = TRUE,col=c("skyblue","red"))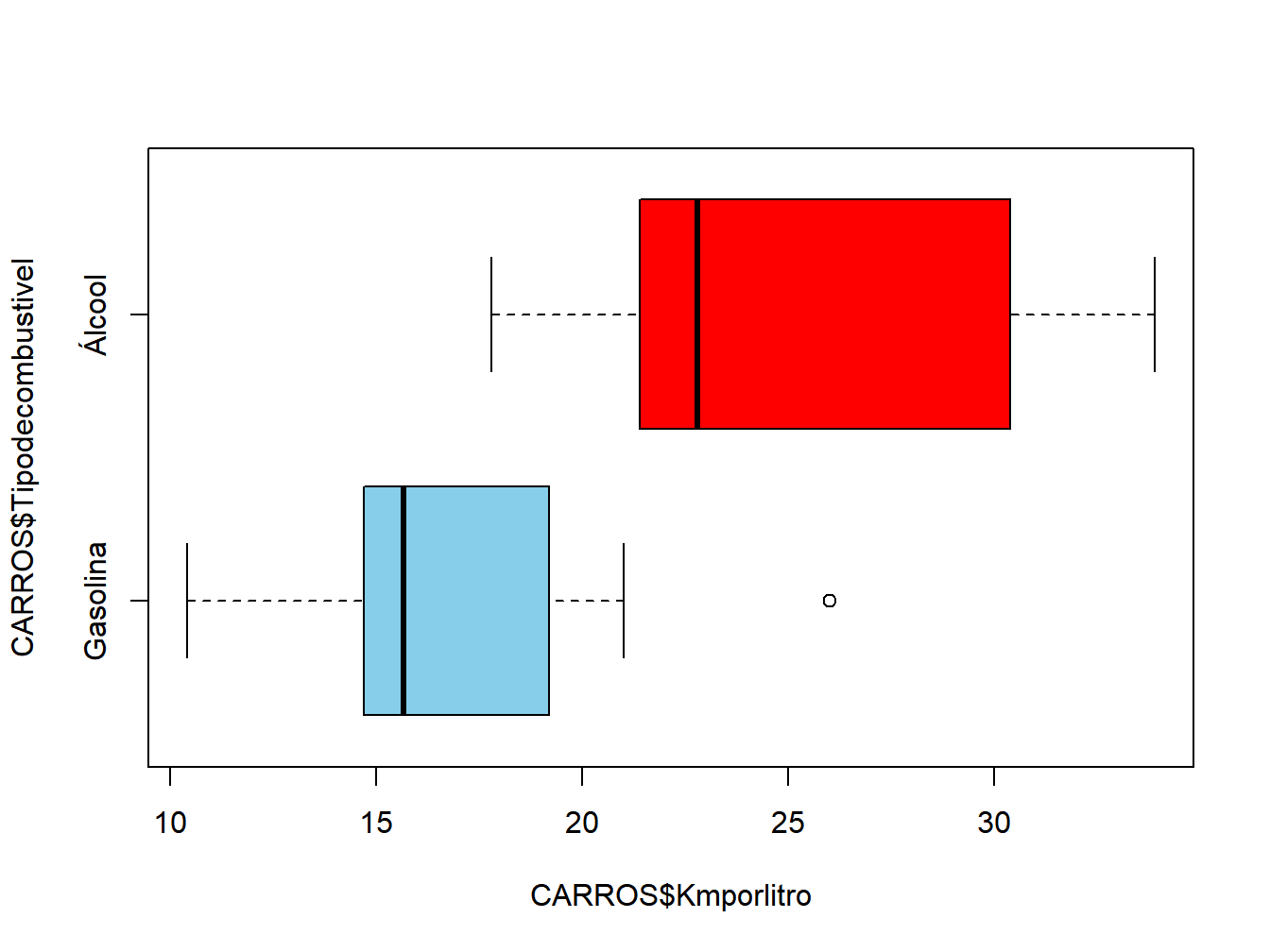

Figura 12.3: Teste

#### Teste t de Student com variâncias desiguais (Teste-t de Welch)
t.test(CARROS$Kmporlitro~CARROS$Tipodecombustivel, var.equal=FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  CARROS$Kmporlitro by CARROS$Tipodecombustivel
## t = -4.6671, df = 22.716, p-value = 0.0001098
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -11.462508  -4.418445
## sample estimates:
## mean in group Gasolina   mean in group Álcool 
##               16.61667               24.55714

12.1.3 Análise de Variância - ANOVA

A ANOVA é parecida com o teste t de Student, mas pode comparar mais de duas médias e mostra se as diferenças entre essas médias são significativas. Este teste permite que você avalie se a diferença entre as médias ocorreram por acaso ou não.

Este teste deve ser utilizado somente após a avaliação dos pressupostos de Normalidade, de homogeneidade de variâncias (variâncias iguais), e independência. Ele e realizado com a função aov.

Utiliza-se este teste quando:
* Os dados seguem a Distribuição normal;
* Temos dois grupos ou mais;
* Concluimos no teste de Bartlett que os grupos têm variâncias iguais.

12.1.3.1 Dados apropriados

• A variável dependente é quantitativa.
• A variável independente é qualitativa.

12.1.3.2 Hipóteses

Hipótese nula: \[ \mu_1 = \mu_2 = \mu_3 = ... = \mu_k \] (as médias são iguais)
Hipótese alternativa: \[ \mu_i \neq \mu_j \] (pelo menos uma média diferente para qualquer i e j).

12.1.3.3 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa entre pelo menos duas médias. Devemos realizar os testes post hoc”.

12.1.3.4 Exemplo da ANOVA

#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
                      "Amperagem_circ_eletrico","Peso","RPM",
                      "Tipodecombustivel","TipodeMarcha",
                      "NumdeMarchas","NumdeValvulas")
CARROS$Cilindros<-as.factor(CARROS$Cilindros)

### Verifique os dados
str(CARROS$Kmporlitro)

##  num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...

str(CARROS$Cilindros)

##  Factor w/ 3 levels "4","6","8": 2 2 1 2 3 2 3 1 1 2 ...

levels(CARROS$Cilindros)

## [1] "4" "6" "8"

### Remova objetos desnecessários
remove(mtcars)

#### Resumo dos dados 
library(psych)
describeBy(CARROS$Kmporlitro,group = CARROS$Cilindros)

## 
##  Descriptive statistics by group 
## group: 4
##    vars  n  mean   sd median trimmed  mad  min  max range skew kurtosis   se
## X1    1 11 26.66 4.51     26   26.44 6.52 21.4 33.9  12.5 0.26    -1.65 1.36
## ------------------------------------------------------------ 
## group: 6
##    vars n  mean   sd median trimmed  mad  min  max range  skew kurtosis   se
## X1    1 7 19.74 1.45   19.7   19.74 1.93 17.8 21.4   3.6 -0.16    -1.91 0.55
## ------------------------------------------------------------ 
## group: 8
##    vars  n mean   sd median trimmed  mad  min  max range  skew kurtosis   se
## X1    1 14 15.1 2.56   15.2   15.15 1.56 10.4 19.2   8.8 -0.36    -0.57 0.68

#### Box-plot
boxplot(CARROS$Kmporlitro~CARROS$Cilindros,
        horizontal = TRUE,col=c("skyblue","red","green"))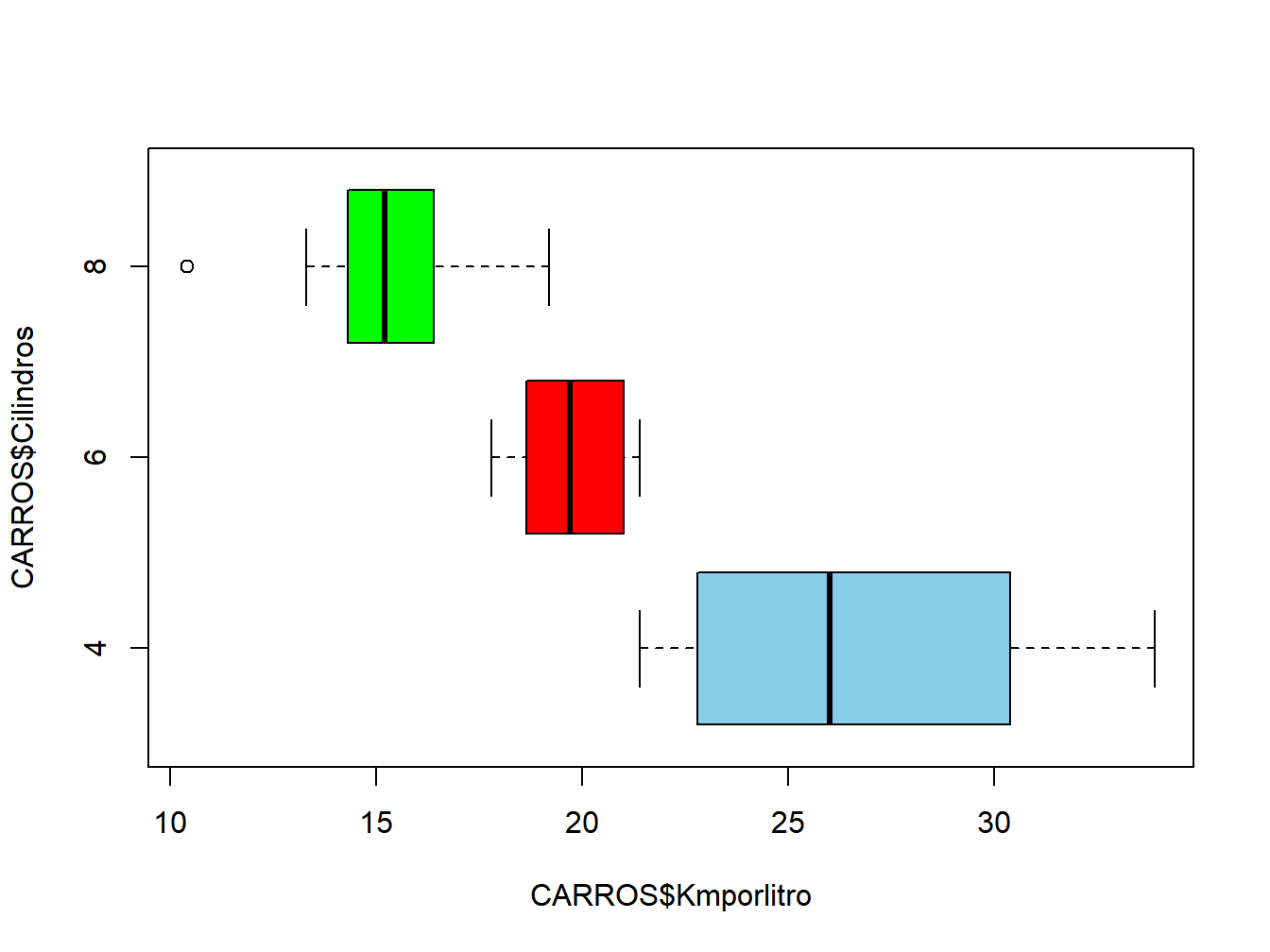

Figura 12.4: Teste

#### Verificando os pressupostos de normalidade (resíduos com 
# distribuição normal) e homogeneidade de variâncias (variância 
# constante) 
modelo <- aov(Kmporlitro~Cilindros,data = CARROS)
residuos<-residuals(modelo)
shapiro.test(residuos)

## 
##  Shapiro-Wilk normality test
## 
## data:  residuos
## W = 0.97065, p-value = 0.5177

bartlett.test(residuos~CARROS$Cilindros)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  residuos by CARROS$Cilindros
## Bartlett's K-squared = 8.3934, df = 2, p-value = 0.01505

#### Os residuos tem distribuição normal, mas a variancia 
# não é constante.
# vamos fazer uma transformação LOG
modelo2 <- aov(log(Kmporlitro)~Cilindros,data = CARROS)
residuos<-residuals(modelo2)
shapiro.test(residuos)

## 
##  Shapiro-Wilk normality test
## 
## data:  residuos
## W = 0.96444, p-value = 0.3616

bartlett.test(residuos~CARROS$Cilindros)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  residuos by CARROS$Cilindros
## Bartlett's K-squared = 4.7326, df = 2, p-value = 0.09383

#### Ótimo! os residuos tem distribuição normal e 
# a variancia é constante.
summary(modelo2)

##             Df Sum Sq Mean Sq F value        Pr(>F)    
## Cilindros    2 2.0081  1.0040   39.31 0.00000000552 ***
## Residuals   29 0.7407  0.0255                          
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A partir deste resultado, podemos ver que a variável cilindros é significativa, mas não sabemos quais das três médias são diferentes entre si.

No entanto, isso exigirá três testes (quatro vs seis, seis vs oito e quatro vs oito), portanto, desejamos mostrar quais dessas diferenças são significativas. Isso pode ser realizado com os testes post-hoc. Os testes post-hoc muitas vezer são chamados de testes a posteriori porque eles devem ser realizados depois da ANOVA.

Podemos ver as diferencas entre as médias e o p-valor usando o comando TukeyHSD (Tukey Honest Significant Differences). Se quiser saber mais, esta é uma ótima referencia

#-------------------------------------------------------------
TukeyHSD(modelo2)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = log(Kmporlitro) ~ Cilindros, data = CARROS)
## 
## $Cilindros
##           diff        lwr         upr     p adj
## 6-4 -0.2900143 -0.4808396 -0.09918904 0.0021808
## 8-4 -0.5702825 -0.7293036 -0.41126146 0.0000000
## 8-6 -0.2802682 -0.4629695 -0.09756690 0.0019875

Podemos ver que as médias de Km/l com 6 e 4, 8 e 4, e 8 e 6 cilindros são significativas.

12.1.4 ANOVA de Welch

Um procedimento considerado equivalente a transformação dos dados é a Anova de Welch para variâncias desiguais.

12.1.4.1 Dados apropriados

A variável dependente é quantitativa.
A variável independente é qualitativa.

12.1.4.2 Hipóteses

Hipótese nula: \[ \mu_1 = \mu_2 = \mu_3 = ... = \mu_k \] (as médias são iguais)
Hipótese alternativa: \[ \mu_i \neq \mu_j \] (pelo menos uma média diferente para qualquer i e j).

12.1.4.3 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa entre pelo menos duas médias.”.

12.1.4.4 Exemplo da ANOVA de Welch

#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
                      "Amperagem_circ_eletrico","Peso","RPM",
                      "Tipodecombustivel","TipodeMarcha",
                      "NumdeMarchas","NumdeValvulas")
CARROS$Cilindros<-as.factor(CARROS$Cilindros)

### Verifique os dados
str(CARROS$Kmporlitro)

##  num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...

str(CARROS$Cilindros)

##  Factor w/ 3 levels "4","6","8": 2 2 1 2 3 2 3 1 1 2 ...

levels(CARROS$Cilindros)

## [1] "4" "6" "8"

### Remova objetos desnecessários
remove(mtcars)

#### Resumo dos dados 
library(psych)
describeBy(CARROS$Kmporlitro,group = CARROS$Cilindros)

## 
##  Descriptive statistics by group 
## group: 4
##    vars  n  mean   sd median trimmed  mad  min  max range skew kurtosis   se
## X1    1 11 26.66 4.51     26   26.44 6.52 21.4 33.9  12.5 0.26    -1.65 1.36
## ------------------------------------------------------------ 
## group: 6
##    vars n  mean   sd median trimmed  mad  min  max range  skew kurtosis   se
## X1    1 7 19.74 1.45   19.7   19.74 1.93 17.8 21.4   3.6 -0.16    -1.91 0.55
## ------------------------------------------------------------ 
## group: 8
##    vars  n mean   sd median trimmed  mad  min  max range  skew kurtosis   se
## X1    1 14 15.1 2.56   15.2   15.15 1.56 10.4 19.2   8.8 -0.36    -0.57 0.68

#### Box-plot
boxplot(CARROS$Kmporlitro~CARROS$Cilindros,
        horizontal = TRUE,col=c("skyblue","red","green"))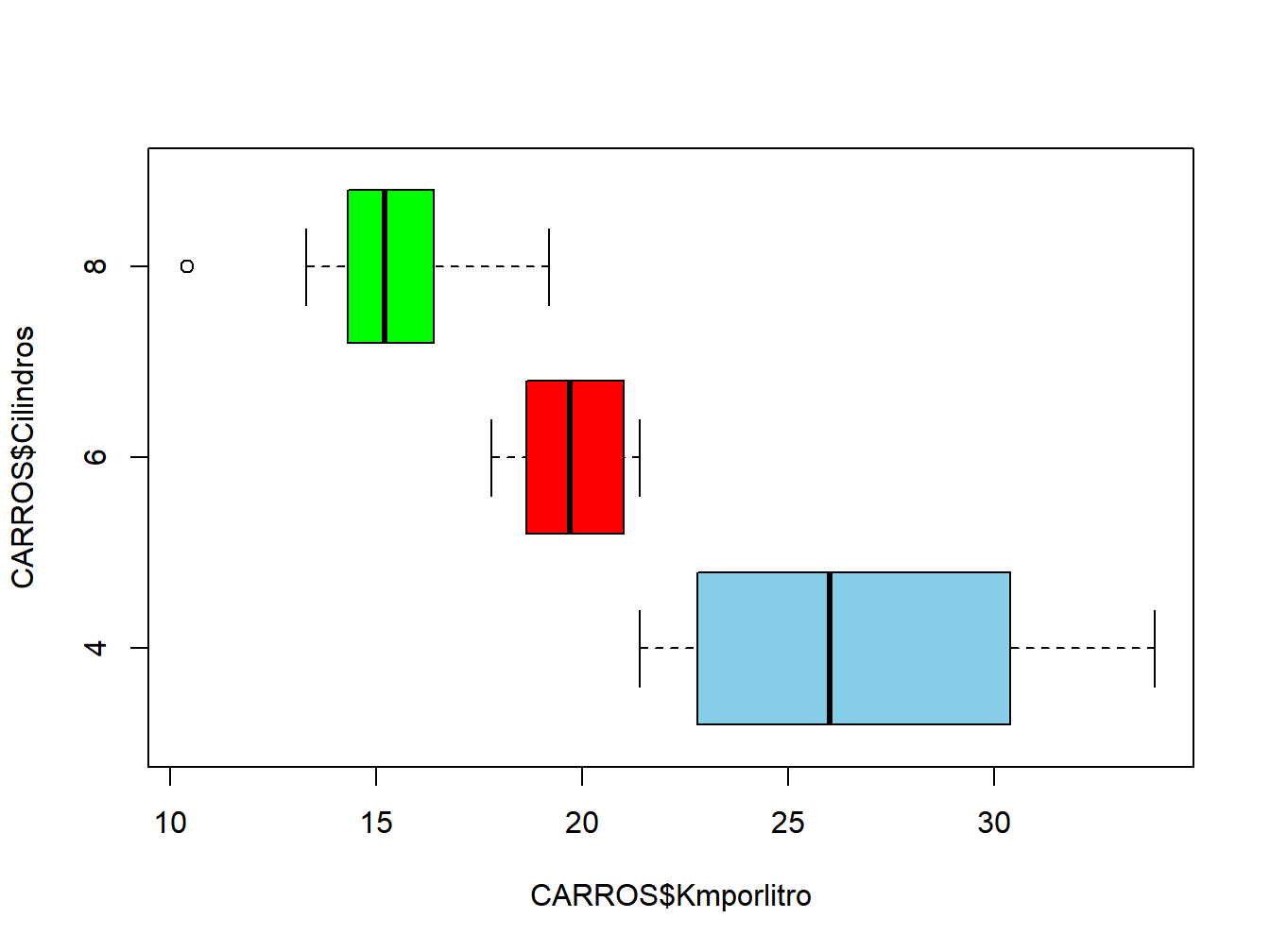

Figura 12.5: Teste

#### Verificando os pressupostos de normalidade (resíduos com 
# distribuição normal) e homogeneidade de variâncias (variância 
# constante) 
modelo <- aov(Kmporlitro~Cilindros,data = CARROS)
residuos<-residuals(modelo)
shapiro.test(residuos)

## 
##  Shapiro-Wilk normality test
## 
## data:  residuos
## W = 0.97065, p-value = 0.5177

bartlett.test(residuos~CARROS$Cilindros)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  residuos by CARROS$Cilindros
## Bartlett's K-squared = 8.3934, df = 2, p-value = 0.01505

#### Os residuos tem distribuição normal, mas a variancia 
# não é constante.
# vamos utilizar a ANOVA de Welch 

modelo2 <- oneway.test(Kmporlitro~Cilindros,data = CARROS)
modelo2

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  Kmporlitro and Cilindros
## F = 31.624, num df = 2.000, denom df = 18.032, p-value = 0.000001271

o comando TukeyHSD não funciona com a ANOVA de Welch. Ainda não encontrei um pacote do R para facilitar a aplicação dos teste post-hoc. Desso modo, vou deixar a discussão sobre como implementar esses testes aqui

12.1.5 ANOVA em Blocos

A ANOVA em Blocos determina se há diferenças entre os grupos em um design de blocos. Nesse tipo de projeto, temos duas variáveis independentes: uma variável que serve como tratamento ou grupo e a outra serve como variável de bloco.

É nas diferenças entre tratamentos ou grupos que estamos interessados. Não estamos interessados nas diferenças entre os blocos, mas queremos que nossas estatísticas levem em conta as diferenças nos blocos (controle o efeito do bloco).

#-------------------------------------------------------------
# ANOVA com Blocos
tratamento   <- factor(rep(1:4, each = 4))
bloco <- factor(rep(1:4, times = 4))
y <- c(9.3, 9.4, 9.6, 10, 9.4, 9.3, 9.8, 9.9,
       9.2, 9.4, 9.5, 9.7,9.7, 9.6, 10, 10.2)
banco <- data.frame(y, tratamento, bloco)
## Analyze data ####
modelo <- aov(y ~ tratamento + bloco, data = banco)                 
summary(modelo)

##             Df Sum Sq Mean Sq F value    Pr(>F)    
## tratamento   3  0.385 0.12833   14.44  0.000871 ***
## bloco        3  0.825 0.27500   30.94 0.0000452 ***
## Residuals    9  0.080 0.00889                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.1.6 ANOVA com dois fatores: o desenho fatorial

Esse seguimento é uma tentativa de tradução do livro Mangiafico (2015). Se você quiser ler o documento original, clique aqui

A ANOVA com dois fatores geralmente vêm de experimentos com um planejamento fatorial. Um planejamento fatorial possui pelo menos duas variáveis independentes.

O exemplo de ganho de peso abaixo mostra dados fatoriais. Neste exemplo, existem três observações para cada combinação de dieta e país.

Com esse tipo de dado, geralmente estamos interessados em testar o efeito de cada variável independente (efeitos principais) e depois o efeito de sua combinação (efeito de interação).

Um modo de ver esse efeito é por meio do gráfico de interação. Ele mostra o valor médio ou mediano da variável de resposta para cada combinação das variáveis independentes. Esse tipo de gráfico, especialmente se incluir barras de erro para indicar a variabilidade dos dados dentro de cada grupo, nos dá uma compreensão do efeito dos principais fatores e de sua interação.

Quando a interação é significativa, não podemos realizar testes post-hoc para os efeitos principais. Os resultados podem ser mascarados pelo efeito da interação. Com um desenho fatorial, existem diretrizes para determinar quando fazer testes post-hoc. De uma forma simplificada, as diretrizes são apresentadas a seguir:

• Quando nem os efeitos principais nem o efeito de interação são estatisticamente significativos, nenhum teste post-hoc de separação média deve ser realizado.
• Quando um ou mais dos efeitos principais são estatisticamente significativos e o efeito da interação tem o p-valor acima de 0,05, os testes pós-hoc devem ser realizado apenas com efeitos principais significativos. • Quando o efeito da interação é estatisticamente significativo, os testes pós-hoc devem ser realizado apenas no efeito da interação. Este é o caso mesmo quando os principais efeitos também são estatisticamente significativos. Isso porque os efeitos principais podem ser mascarados pelo efeito da interação.

12.1.6.1 Exemplo ANOVA com dois fatores sem efeito de interação

Imagine para este exemplo um experimento em que as pessoas foram submetidas a uma das três dietas para incentivar a perda de peso. O peso ganho será a variável dependente quantitativa. Temos duas variáveis independentes: 1. a variável categórica chamada dieta com três níveis diferentes e 2. o país em que os indivíduos vivem (variável categórica com dois níveis).

Esse tipo de análise faz certas suposições sobre a distribuição dos dados (linearidade, independência, normalidade e homocedasticidade), mas, por simplicidade, este exemplo ignorará a necessidade de determinar se os dados atendem a essas suposições.

#-------------------------------------------------------------
Entrada =("
dieta    pais  mudanca_peso
 A       BR      0.120
 A       BR      0.125
 A       BR      0.112
 A       UK      0.052
 A       UK      0.055
 A       UK      0.044
 B       BR      0.096
 B       BR      0.100
 B       BR      0.089
 B       UK      0.025
 B       UK      0.029
 B       UK      0.019
 C       BR      0.149
 C       BR      0.150
 C       BR      0.142
 C       UK      0.077
 C       UK      0.080
 C       UK      0.066
")

Dados <- read.table(textConnection(Entrada),header=TRUE)

### Transfomar character em categórica
Dados$pais <- as.factor(Dados$pais)
Dados$dieta <- as.factor(Dados$dieta)

### Verifique os dados
str(Dados)

## 'data.frame':    18 obs. of  3 variables:
##  $ dieta       : Factor w/ 3 levels "A","B","C": 1 1 1 1 1 1 2 2 2 2 ...
##  $ pais        : Factor w/ 2 levels "BR","UK": 1 1 1 2 2 2 1 1 1 2 ...
##  $ mudanca_peso: num  0.12 0.125 0.112 0.052 0.055 0.044 0.096 0.1 0.089 0.025 ...

### Remova objetos desnecessários
remove(Entrada)

12.1.6.2 Gráfico de interação

A função action.plot cria um gráfico de interação simples para dados com duas independentes categóricas. Para o significado das opções, consulte ?action.plot.

Esse estilo de gráfico de interação não mostra a variabilidade da média de cada grupo, portanto, é difícil usar esse estilo de gráfico para determinar se há diferenças significativas entre os grupos.

O gráfico mostra que o ganho de peso médio para cada dieta foi menor no Reino Unido em comparação com o Brasil. E que essa diferença era relativamente constante para cada dieta, como é evidenciado pelas linhas paralelas na trama. Isso sugere que não há efeito de interação grande ou significativo. Ou seja, a diferença entre as dietas é constante entre os países.

#-------------------------------------------------------------
interaction.plot(x.factor     = Dados$pais,
                 trace.factor = Dados$dieta,
                 response     = Dados$mudanca_peso,
                 fun = mean,type="b",
                 col=c("black","red","green"),  
                 pch=c(19, 17, 15),             
                 fixed=TRUE,leg.bty = "o")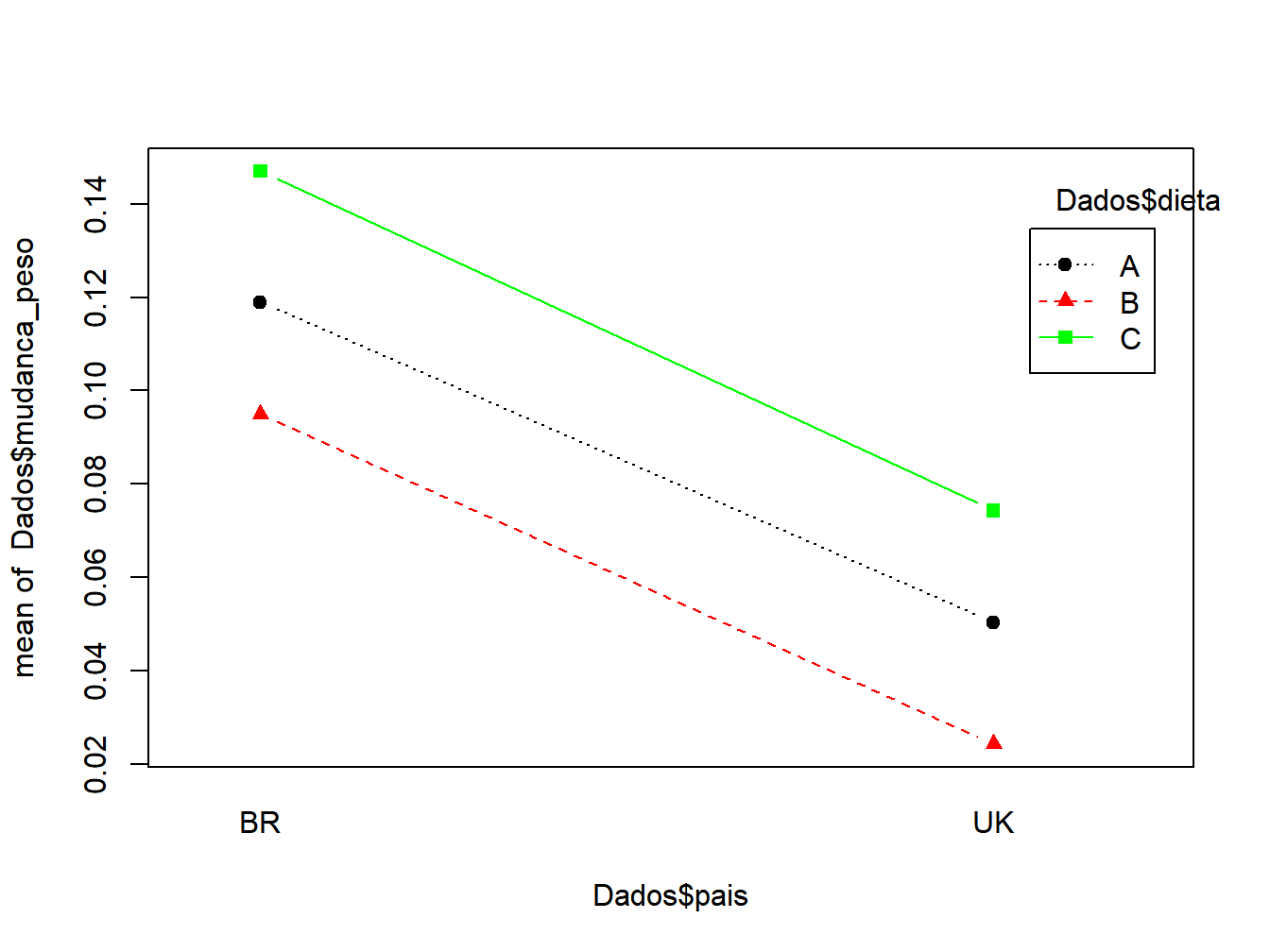

Figura 12.6: interação

12.1.6.3 Como especificar o modelo linear e realizar uma ANOVA

O modelo linear é especificado com: * a variável dependente (y) é a mudanca_peso. * as variáveis independentes são país e dieta. e * o termo de interação para país e dieta é adicionada ao modelo ( país:dieta).

A tabela ANOVA indica que os efeitos principais (efeitos das variáveis) são significativos, mas que o efeito de interação não é.

#-------------------------------------------------------------
# Two Way Factorial Design
modelo <-aov(mudanca_peso ~ dieta + pais + dieta:pais,data = Dados)
#forma alternativa
#modelo <-aov(mudanca_peso ~ dieta*pais,data = Dados)
summary(modelo)

##             Df   Sum Sq  Mean Sq F value           Pr(>F)    
## dieta        2 0.007804 0.003902 114.205 0.00000001546589 ***
## pais         1 0.022472 0.022472 657.717 0.00000000000752 ***
## dieta:pais   2 0.000012 0.000006   0.176            0.841    
## Residuals   12 0.000410 0.000034                             
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.1.6.4 Teste post-hoc com lsmeans

Como os efeitos principais foram significativos, queremos realizar testes de comparação par-a-par (post-hoc) para cada variável independente (efeito principal).

Para isso, usaremos o pacote lsmeans. A fórmula na função lsmeans indica que comparações aos pares devem ser realizadas para a variável País e para a variável Dieta.

#-------------------------------------------------------------

library(lsmeans)

lsmeans(modelo,
        pairwise ~ pais,
        adjust="tukey")

## $lsmeans
##  pais lsmean      SE df lower.CL upper.CL
##  BR   0.1203 0.00195 12   0.1154   0.1253
##  UK   0.0497 0.00195 12   0.0447   0.0546
## 
## Results are averaged over the levels of: dieta 
## Confidence level used: 0.95 
## Conf-level adjustment: sidak method for 2 estimates 
## 
## $contrasts
##  contrast estimate      SE df t.ratio p.value
##  BR - UK    0.0707 0.00276 12 25.646  <.0001 
## 
## Results are averaged over the levels of: dieta

lsmeans(modelo,
        pairwise ~ dieta,
        adjust="tukey")

## $lsmeans
##  dieta lsmean      SE df lower.CL upper.CL
##  A     0.0847 0.00239 12   0.0781   0.0913
##  B     0.0597 0.00239 12   0.0531   0.0663
##  C     0.1107 0.00239 12   0.1041   0.1173
## 
## Results are averaged over the levels of: pais 
## Confidence level used: 0.95 
## Conf-level adjustment: sidak method for 3 estimates 
## 
## $contrasts
##  contrast estimate      SE df t.ratio p.value
##  A - B       0.025 0.00337 12   7.408 <.0001 
##  A - C      -0.026 0.00337 12  -7.704 <.0001 
##  B - C      -0.051 0.00337 12 -15.112 <.0001 
## 
## Results are averaged over the levels of: pais 
## P value adjustment: tukey method for comparing a family of 3 estimates

12.1.6.5 Exemplo ANOVA com dois fatores com efeito de interação

Vamos usar o mesmo exemplo, mas vamos colocar um país a mais: a Argentina

#-------------------------------------------------------------
Entrada =("
dieta    pais  mudanca_peso
 A       BR      0.120
 A       BR      0.125
 A       BR      0.112
 A       UK      0.052
 A       UK      0.055
 A       UK      0.044
 A       AR      0.080
 A       AR      0.090
 A       AR      0.075
 B       BR      0.096
 B       BR      0.100
 B       BR      0.089
 B       UK      0.025
 B       UK      0.029
 B       UK      0.019
 B       AR      0.055
 B       AR      0.065
 B       AR      0.050
 C       BR      0.149
 C       BR      0.150
 C       BR      0.142
 C       UK      0.077
 C       UK      0.080
 C       UK      0.066
 C       AR      0.055
 C       AR      0.065
 C       AR      0.050
 C       AR      0.054
")


Dados <- read.table(textConnection(Entrada),header=TRUE)

### Transfomar character em categórica
Dados$pais <- as.factor(Dados$pais)
Dados$dieta <- as.factor(Dados$dieta)

### Verifique os dados
str(Dados)

## 'data.frame':    28 obs. of  3 variables:
##  $ dieta       : Factor w/ 3 levels "A","B","C": 1 1 1 1 1 1 1 1 1 2 ...
##  $ pais        : Factor w/ 3 levels "AR","BR","UK": 2 2 2 3 3 3 1 1 1 2 ...
##  $ mudanca_peso: num  0.12 0.125 0.112 0.052 0.055 0.044 0.08 0.09 0.075 0.096 ...

### Remova objetos desnecessários
remove(Entrada)

12.1.6.6 Gráfico de interação

O gráfico sugere que o efeito da dieta não é consistente nos três países. Embora a Dieta C tenha apresentado o maior ganho médio de peso para o Brasil e o Reino Unido, para a Argentina ela tem uma média menor que a Dieta A. Isso sugere que pode haver um efeito de interação significativo, mas precisaremos fazer um teste estatístico para confirmar esta hipótese .

#-------------------------------------------------------------
interaction.plot(x.factor     = Dados$pais,
                 trace.factor = Dados$dieta,
                 response     = Dados$mudanca_peso,
                 fun = mean,type="b",
                 col=c("black","red","green"),  
                 pch=c(19, 17, 15),             
                 fixed=TRUE,leg.bty = "o")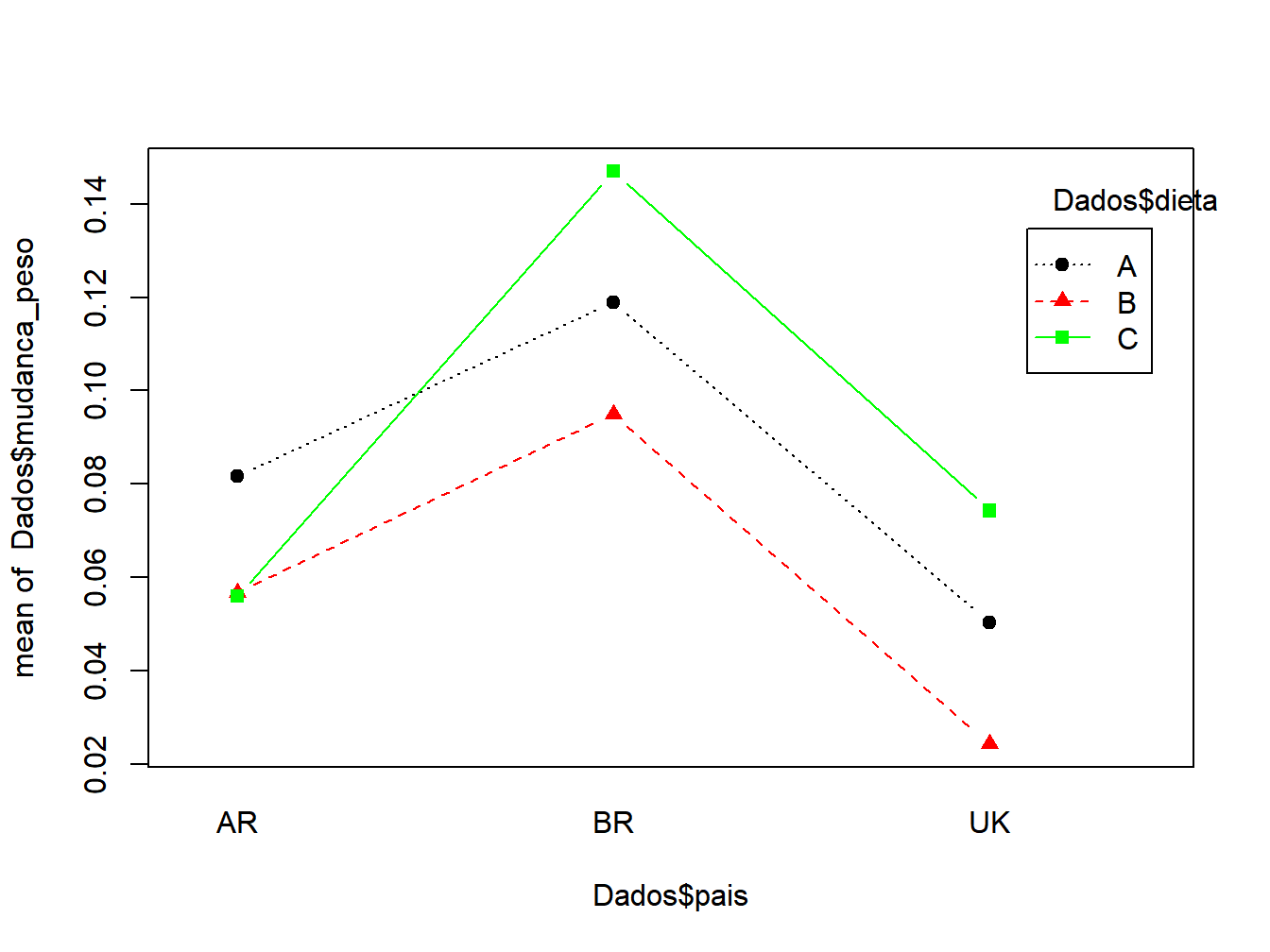

Figura 12.7: interação

A tabela ANOVA indica que os efeitos principais e o efeito de interação são significativos.

#-------------------------------------------------------------
# Two Way Factorial Design
modelo <-aov(mudanca_peso ~ dieta + pais + dieta:pais,data = Dados)
#forma alternativa
#modelo <-aov(mudanca_peso ~ dieta*pais,data = Dados)
summary(modelo)

##             Df   Sum Sq  Mean Sq F value              Pr(>F)    
## dieta        2 0.004811 0.002406   59.72 0.00000000639732710 ***
## pais         2 0.025676 0.012838  318.71 0.00000000000000243 ***
## dieta:pais   4 0.004016 0.001004   24.93 0.00000024772486736 ***
## Residuals   19 0.000765 0.000040                                
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.1.6.7 Teste post-hoc com lsmeans

Como o efeito da interação foi significativo, gostaríamos de comparar todas as médias de grupos da interação. Embora os efeitos principais tenham sido significativos, o conselho típico é não realizar comparações aos pares dos efeitos principais quando a interação deles for significativa. Isso ocorre porque o foco nos grupos na interação descreve melhor os resultados da análise.

Usaremos o mesmo pacote lsmeans e vamos fazer os contrastes para a interação País e Dieta, indicadas com país:dieta.

#-------------------------------------------------------------

library(lsmeans)

marginal <- lsmeans(modelo,
                      pairwise ~ pais:dieta,
                      adjust="tukey")      
marginal$contrasts

##  contrast     estimate      SE df t.ratio p.value
##  AR,A - BR,A -0.037333 0.00518 19  -7.204 <.0001 
##  AR,A - UK,A  0.031333 0.00518 19   6.046 0.0002 
##  AR,A - AR,B  0.025000 0.00518 19   4.824 0.0030 
##  AR,A - BR,B -0.013333 0.00518 19  -2.573 0.2600 
##  AR,A - UK,B  0.057333 0.00518 19  11.064 <.0001 
##  AR,A - AR,C  0.025667 0.00485 19   5.295 0.0011 
##  AR,A - BR,C -0.065333 0.00518 19 -12.608 <.0001 
##  AR,A - UK,C  0.007333 0.00518 19   1.415 0.8786 
##  BR,A - UK,A  0.068667 0.00518 19  13.251 <.0001 
##  BR,A - AR,B  0.062333 0.00518 19  12.029 <.0001 
##  BR,A - BR,B  0.024000 0.00518 19   4.631 0.0045 
##  BR,A - UK,B  0.094667 0.00518 19  18.268 <.0001 
##  BR,A - AR,C  0.063000 0.00485 19  12.997 <.0001 
##  BR,A - BR,C -0.028000 0.00518 19  -5.403 0.0009 
##  BR,A - UK,C  0.044667 0.00518 19   8.619 <.0001 
##  UK,A - AR,B -0.006333 0.00518 19  -1.222 0.9414 
##  UK,A - BR,B -0.044667 0.00518 19  -8.619 <.0001 
##  UK,A - UK,B  0.026000 0.00518 19   5.017 0.0020 
##  UK,A - AR,C -0.005667 0.00485 19  -1.169 0.9539 
##  UK,A - BR,C -0.096667 0.00518 19 -18.654 <.0001 
##  UK,A - UK,C -0.024000 0.00518 19  -4.631 0.0045 
##  AR,B - BR,B -0.038333 0.00518 19  -7.397 <.0001 
##  AR,B - UK,B  0.032333 0.00518 19   6.239 0.0002 
##  AR,B - AR,C  0.000667 0.00485 19   0.138 1.0000 
##  AR,B - BR,C -0.090333 0.00518 19 -17.432 <.0001 
##  AR,B - UK,C -0.017667 0.00518 19  -3.409 0.0577 
##  BR,B - UK,B  0.070667 0.00518 19  13.637 <.0001 
##  BR,B - AR,C  0.039000 0.00485 19   8.046 <.0001 
##  BR,B - BR,C -0.052000 0.00518 19 -10.035 <.0001 
##  BR,B - UK,C  0.020667 0.00518 19   3.988 0.0177 
##  UK,B - AR,C -0.031667 0.00485 19  -6.533 0.0001 
##  UK,B - BR,C -0.122667 0.00518 19 -23.671 <.0001 
##  UK,B - UK,C -0.050000 0.00518 19  -9.649 <.0001 
##  AR,C - BR,C -0.091000 0.00485 19 -18.773 <.0001 
##  AR,C - UK,C -0.018333 0.00485 19  -3.782 0.0272 
##  BR,C - UK,C  0.072667 0.00518 19  14.023 <.0001 
## 
## P value adjustment: tukey method for comparing a family of 9 estimates

# Gráfico de interação com o pacote phia
#O pacote phia pode ser usado para criar gráficos de interação. 
library(phia)

# Divide o dispositivo gráfico em 04 gráficos por janela
par(mfrow=c(2,2))
IM <- interactionMeans(modelo)

### Gráfico de interação
plot(IM)

### Retorne o dispositivo gráfico ao seu estado original
#de um gráfico por janela
par(mfrow=c(1,1))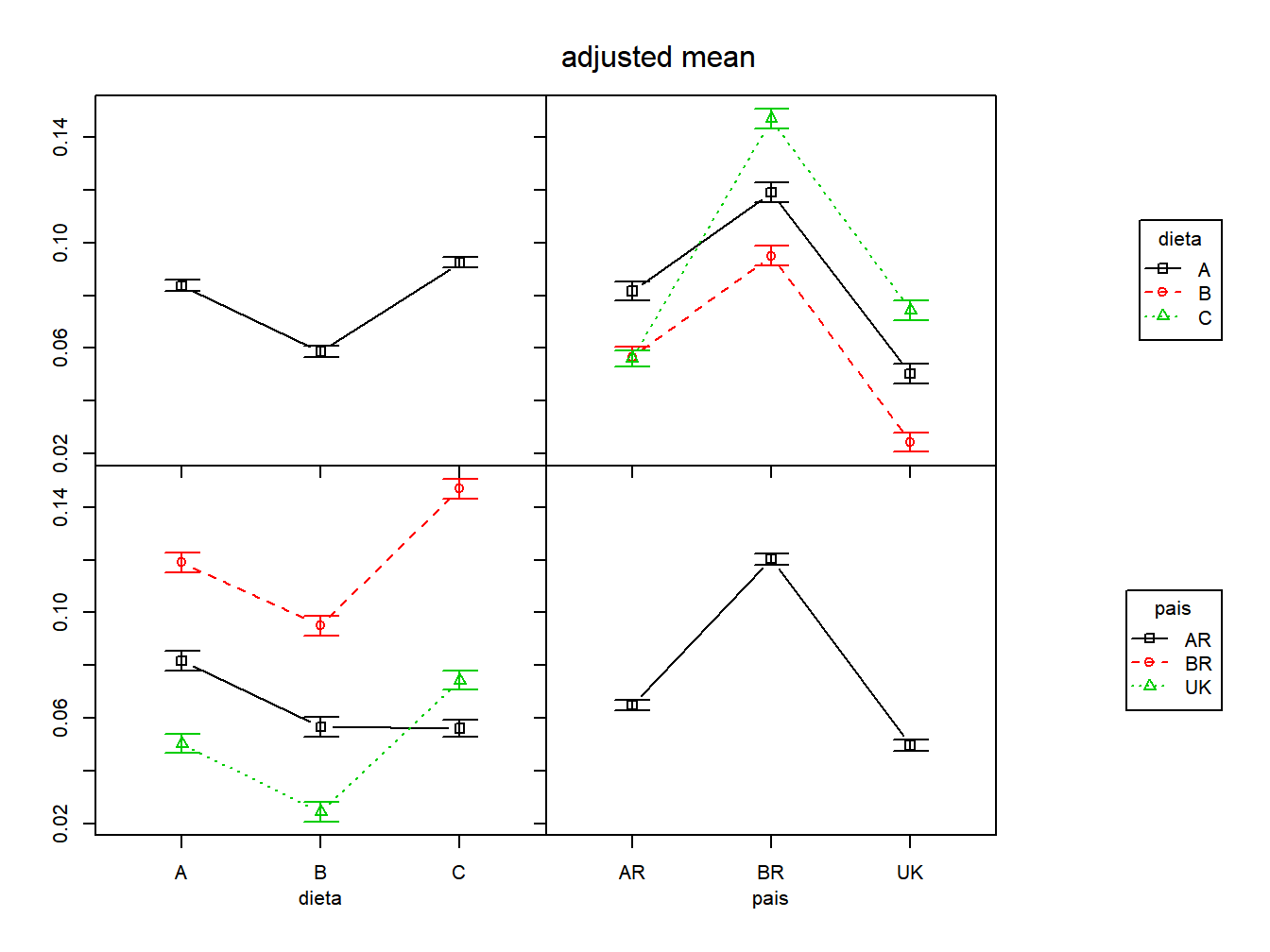

Figura 12.8: gráfico de interação

12.1.6.8 Indo além: outros tipos de ANOVA

Existem muitos outros tipos de ANOVA. Como por exemplo:

Experimentos em parcelas subdivididas (split-plot)
ANCOVA - Análise de Covariância
MANOVA - Análise multivariada da variância
ANOVA com medidas repetidas

Todos esses modelos são utilizados em estatística experimental. Um bom livro em R sobre os outros modelos ANOVAs pode ser encontrado aqui.

Um livro de referência para essa área é o livro do (Montgomery 2019) chamado Design and Analysis of Experiments. Vou apenas apresentar os comandos para a realização desses modelos.

#-------------------------------------------------------------
### Banco de dados
data(iris)

### Verifique os dados
str(iris)

## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

# ANCOVA - Análise de Covariância
# duas variáveis independentes: uma quantitativa e uma qualitativa
fit <- aov(Sepal.Length~Petal.Width+Species, data=iris) 
summary(fit)

##              Df Sum Sq Mean Sq F value              Pr(>F)    
## Petal.Width   1  68.35   68.35 295.427 <0.0000000000000002 ***
## Species       2   0.03    0.02   0.075               0.928    
## Residuals   146  33.78    0.23                                
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# MANOVA - Análise multivariada da variância 
# 3 Variáveis dependentes e uma independente
Y <- cbind(iris$Sepal.Length,iris$Sepal.Width,iris$Petal.Length) 
fit <- manova(Y ~ Species, data=iris)
summary(fit)

##            Df Pillai approx F num Df den Df                Pr(>F)    
## Species     2 1.1325   63.532      6    292 < 0.00000000000000022 ***
## Residuals 147                                                        
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.2 Abordagem não-paramétrica

Quando os pressupostos (normalidade ou homogêneidade de variâncias) são violados, é comum procurar um método não-paramétrico. A tabela a seguir mostra os equivalentes não-paramétricos para os procedimentos paramétricos. Em seguida, vamos descrever cada um dos métodos

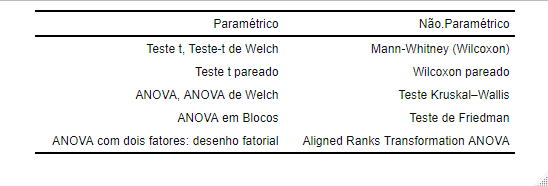
Figura 12.9: Comparação de abordagens

12.2.1 Teste U de Mann-Whitney (Wilcoxon) de duas amostras

Esse seguimento é uma tentativa de tradução do livro Mangiafico (2015). Se você quiser ler o documento original, clique aqui.

12.2.1.1 Quando usar este teste

O teste U de Mann-Whitney (Wilcoxon) de duas amostras é tipicamente um teste de igualdade estocástica entre duas distribuições de dados. Esse teste é baseado em classificação que compara valores para dois grupos. Um resultado significativo sugere que os valores para os dois grupos são diferentes.

Sem outras suposições sobre a distribuição dos dados, o teste de Mann-Whitney não aborda hipóteses sobre as medianas dos grupos. Em vez disso, o teste aborda se é provável que uma observação em um grupo seja maior que uma observação no outro. Às vezes, isso é afirmado como teste se uma amostra possui dominância estocástica em comparação com a outra.

O teste assume que as observações são independentes. Ou seja, não é apropriado para séries temporais, dados emparelhados ou dados de medidas repetidas.

12.2.1.2 Dados apropriados

Dados de duas amostras. Ou seja, dados com apenas dois grupos.

A variável dependente é quantitativa
A variável independente é qualitativa com dois níveis. Ou seja, dois grupos.
As observações entre os grupos são independentes. Evite séries temporais e dados espaciais (geralmente possuem autocorrelação temporal e espacial).

12.2.1.3 Hipóteses

• Hipótese nula: os dois grupos são amostrados de populações com distribuições idênticas.
• Hipótese alternativa: os dois grupos são amostrados de populações com distribuições diferentes.

12.2.1.4 Interpretação

Resultados significativos podem ser relatados como: “Os valores da variável resposta do grupo A foram significativamente diferentes dos do grupo B.”

12.2.1.5 Outras notas e testes alternativos

O teste U de Mann-Whitney (Wilcoxon) pode ser considerado equivalente ao teste de Kruskal-Wallis com apenas dois grupos.

O teste de mediana de Mood compara as medianas de dois grupos. Todavia, o teste de de Mann-Whitney (Wilcoxon) é considerado mais poderoso que o teste de mediana de Mood.

12.2.1.6 Exemplo de teste de Mann-Whitney (Wilcoxon) para duas amostras

Este exemplo apresenta os dados das palestras motivacionais das famílias Stark e Targaryen do Game of Thrones.Após a palestra foi distribuido um questionário para avaliar o palestrante com uma nota de 1 até 5.

Responde à pergunta: “As pontuações dos Stark são significativamente diferentes da família Targaryen?”

O teste de Mann-Whitney (Wilcoxon) é realizado com a função wilcox.test, que produz um p-valor para a hipótese.

Primeiro, os dados são resumidos e examinados usando gráficos de barras para cada grupo.

#-------------------------------------------------------------
### Banco de dados
Entrada <- ("
 Palestrante Nota
 Stark 3
 Stark 5
 Stark 4
 Stark 4
 Stark 4
 Stark 4
 Stark 4
 Stark 4
 Stark 5
 Stark 5
 Targaryen 2
 Targaryen 4
 Targaryen 2
 Targaryen 2
 Targaryen 1
 Targaryen 2
 Targaryen 3
 Targaryen 2
 Targaryen 2
 Targaryen 3
")

Dados <- read.table(textConnection(Entrada), head = TRUE)

#### Crie uma nova variável que seja a nota da avaliação 
# da palestra como um fator ordenado
Dados$Avalicao = as.factor(Dados$Nota)

### Verifique os dados
str(Dados)

## 'data.frame':    20 obs. of  3 variables:
##  $ Palestrante: Factor w/ 2 levels "Stark","Targaryen": 1 1 1 1 1 1 1 1 1 1 ...
##  $ Nota       : int  3 5 4 4 4 4 4 4 5 5 ...
##  $ Avalicao   : Factor w/ 5 levels "1","2","3","4",..: 3 5 4 4 4 4 4 4 5 5 ...

summary(Dados)

##     Palestrante      Nota      Avalicao
##  Stark    :10   Min.   :1.00   1:1     
##  Targaryen:10   1st Qu.:2.00   2:6     
##                 Median :3.50   3:3     
##                 Mean   :3.25   4:7     
##                 3rd Qu.:4.00   5:3     
##                 Max.   :5.00

### Remova objetos desnecessários
rm(Entrada)

Observe que a variável que queremos observar é Avaliação. As contagens para Avaliacao são tabuladas cruzadamente sobre os valores de Palestrante. A função prop.table converte uma tabela em proporções. A opção margem = 1 indica que as proporções são calculadas para cada linha.

#-------------------------------------------------------------
#### Resumo dos dados tratando as pontuações como categórico

# Numero Absoluto
tabela <- table(Dados$Palestrante,Dados$Avalicao)
tabela

##            
##             1 2 3 4 5
##   Stark     0 0 1 6 3
##   Targaryen 1 6 2 1 0

#proporcao
prop.table(tabela,margin = 1)*100

##            
##              1  2  3  4  5
##   Stark      0  0 10 60 30
##   Targaryen 10 60 20 10  0

# As duas medianas
library(psych)
describeBy(Dados$Nota, group = Dados$Palestrante)

## 
##  Descriptive statistics by group 
## group: Stark
##    vars  n mean   sd median trimmed mad min max range  skew kurtosis  se
## X1    1 10  4.2 0.63      4    4.25   0   3   5     2 -0.09    -0.93 0.2
## ------------------------------------------------------------ 
## group: Targaryen
##    vars  n mean   sd median trimmed mad min max range skew kurtosis   se
## X1    1 10  2.3 0.82      2    2.25   0   1   4     3 0.58    -0.45 0.26

12.2.1.7 Exemplo de teste de Mann-Whitney (Wilcoxon) de duas amostras

Este exemplo usa a notação de fórmula indicando que avaliação é a variável dependente e Palestrante é a variável independente. A opção data = indica o banco de dados que contém as variáveis. Para o significado de outras opções, consulte ?Wilcox.test.

#-------------------------------------------------------------

wilcox.test(Nota ~ Palestrante, data = Dados)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  Nota by Palestrante
## W = 95, p-value = 0.0004713
## alternative hypothesis: true location shift is not equal to 0

12.2.2 Teste de Kruskal-Wallis

O teste de Kruskal-Wallis é um teste semelhante ao teste de Mann-Whitney (Wilcoxon), mas pode ser aplicado a variáveis categóricas com mais de dois grupos.

Sem outras suposições sobre a distribuição dos dados, o teste de Kruskal-Wallis não aborda hipóteses sobre as medianas dos grupos. Em vez disso, o teste aborda se é provável que uma observação em um grupo seja maior que uma observação no outro.

O teste assume que as observações são independentes. Ou seja, não é apropriado para observações emparelhadas ou dados de medidas repetidas. É realizado com a função kruskal.test.

12.2.2.1 Testes post-hoc

O resultado do teste de Kruskal-Wallis informa se existem diferenças entre os grupos, mas não informa quais grupos são diferentes de outros grupos. Para determinar quais grupos são diferentes dos outros, é possível realizar testes post-hoc.

12.2.2.2 Dados apropriados

• A variável dependente é ordinal, discreta ou continua.
• Variável independente é um fator com três ou mais níveis. Ou seja, três ou mais grupos.
• As observações entre os grupos são independentes.

12.2.2.3 Hipóteses

• Hipótese nula: os grupos são amostrados de populações com distribuições idênticas. • Hipótese alternativa: os grupos são amostrados de populações com diferentes distribuições.

12.2.2.4 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa nos valores entre os grupos”. Os grupos tem distribuições diferentes.

A análise post-hoc permite dizer “Houve uma diferença significativa nos valores entre os grupos A e B.” e assim por diante.

12.2.2.5 Exemplo de teste de Kruskal–Wallis

Este exemplo apresenta os dados das palestras motivacionais das famílias Stark, Targaryen e Lannister do Game of Thrones. Após a palestra foi distribuido um questionário para avaliar o palestrante com uma nota de 1 até 5. Esse teste responde à pergunta: “As pontuações são significativamente diferentes entre os três palestrantes?”

O teste de Kruskal-Wallis é realizado com a função kruskal.test, que produz um p-valor para a hipótese. Primeiro, os dados são resumidos e examinados usando gráficos de barras para cada grupo.

#-------------------------------------------------------------
 
Entrada =("
 Palestrante Nota
 Stark      3
 Stark      5
 Stark      4
 Stark      4
 Stark      4
 Stark      4
 Stark      4
 Stark      4
 Stark      5
 Stark      5
 Targaryen    2
 Targaryen    4
 Targaryen    2
 Targaryen    2
 Targaryen    1
 Targaryen    2
 Targaryen    3
 Targaryen    2
 Targaryen    2
 Targaryen    3
 Lannister    4
 Lannister    4
 Lannister    4
 Lannister    4
 Lannister    5
 Lannister    3
 Lannister    5
 Lannister    4
 Lannister    4
 Lannister    3
")

Dados <- read.table(textConnection(Entrada), head = TRUE)

#### Crie uma nova variável que seja a categórica
Dados$Avaliacao <- as.factor(Dados$Nota)

### Verifique os dados
str(Dados)

## 'data.frame':    30 obs. of  3 variables:
##  $ Palestrante: Factor w/ 3 levels "Lannister","Stark",..: 2 2 2 2 2 2 2 2 2 2 ...
##  $ Nota       : int  3 5 4 4 4 4 4 4 5 5 ...
##  $ Avaliacao  : Factor w/ 5 levels "1","2","3","4",..: 3 5 4 4 4 4 4 4 5 5 ...

summary(Dados)

##     Palestrante      Nota     Avaliacao
##  Lannister:10   Min.   :1.0   1: 1     
##  Stark    :10   1st Qu.:3.0   2: 6     
##  Targaryen:10   Median :4.0   3: 5     
##                 Mean   :3.5   4:13     
##                 3rd Qu.:4.0   5: 5     
##                 Max.   :5.0

### Remova objetos desnecessários
rm(Entrada)

#### Resumo dos dados tratando as pontuações como categóricas
# Numero Absoluto
tabela <- table(Dados$Palestrante,Dados$Avaliacao)
tabela

##            
##             1 2 3 4 5
##   Lannister 0 0 2 6 2
##   Stark     0 0 1 6 3
##   Targaryen 1 6 2 1 0

#proporcao
prop.table(tabela,margin = 1)*100

##            
##              1  2  3  4  5
##   Lannister  0  0 20 60 20
##   Stark      0  0 10 60 30
##   Targaryen 10 60 20 10  0

# As três medianas
library(psych)
describeBy(Dados$Nota, group = Dados$Palestrante)

## 
##  Descriptive statistics by group 
## group: Lannister
##    vars  n mean   sd median trimmed mad min max range skew kurtosis   se
## X1    1 10    4 0.67      4       4   0   3   5     2    0    -0.97 0.21
## ------------------------------------------------------------ 
## group: Stark
##    vars  n mean   sd median trimmed mad min max range  skew kurtosis  se
## X1    1 10  4.2 0.63      4    4.25   0   3   5     2 -0.09    -0.93 0.2
## ------------------------------------------------------------ 
## group: Targaryen
##    vars  n mean   sd median trimmed mad min max range skew kurtosis   se
## X1    1 10  2.3 0.82      2    2.25   0   1   4     3 0.58    -0.45 0.26

Este exemplo usa a notação de fórmula indicando que Nota é a variável dependente e Palestrante é a variável independente. A opção data = indica o quadro de dados que contém as variáveis. Para o significado de outras opções, consulte ?kruskal.test.

#-------------------------------------------------------------
kruskal.test(Nota ~ Palestrante, data = Dados)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  Nota by Palestrante
## Kruskal-Wallis chi-squared = 16.842, df = 2, p-value = 0.0002202

12.2.2.6 Teste post-hoc: testes de Mann-Whitney para comparações múltiplas

A função pairwise.wilcox.test produz uma tabela de p-valor comparando cada par de grupos. Para evitar a inflação das taxas de erro do tipo I, é possível fazer ajustes no p-valor usando a opção p.adjust.method. O método fdr é usado. Consulte ?p.adjust para obter detalhes sobre os métodos de ajuste de p-valor disponíveis. O código cria uma matriz de p-valor.

12.2.2.7 Pairwise Mann–Whitney

#-------------------------------------------------------------

PMW <- pairwise.wilcox.test(Dados$Nota,
                          Dados$Palestrante,
                          p.adjust.method="fdr")
# Adjusts p-values for multiple comparisons;
# See ?p.adjust for options

PMW

## 
##  Pairwise comparisons using Wilcoxon rank sum test 
## 
## data:  Dados$Nota and Dados$Palestrante 
## 
##           Lannister Stark 
## Stark     0.5174    -     
## Targaryen 0.0012    0.0012
## 
## P value adjustment method: fdr

O p-valor da diferença entre Stark e Lannister é 0,5174. Isso indica que não existe diferença entre as distribuições de notas dessas duas casas.

12.2.3 Teste de Friedman

O teste de Friedman determina se há diferenças entre os grupos em um design de blocos. Nesse projeto, uma variável serve como variável de tratamento ou grupo e outra variável serve como variável de bloco. É nas diferenças entre tratamentos ou grupos que estamos interessados. Não estamos interessados nas diferenças entre os blocos, mas queremos que nossas estatísticas levem em conta as diferenças nos blocos. O teste de Friedman é muitas vezes utilizado como uma análise de variância não-paramétrica com uma variável de bloco. Ou seja, é uma versão não-paramétrica de uma ANOVA com Blocos Aleatorizados.

Isso significa que, embora a ANOVA tem o pressuposto de uma distribuição normal e variâncias iguais (dos resíduos), o teste de Friedman está livre dessas restrições. O preço dessa liberdade paramétrica é a perda de potência (do teste de Friedman em comparação com as versões paramétricas da ANOVA).

Para um exemplo dessa estrutura, veja os dados da família Belcher abaixo.

O avaliador é considerado a variável de bloqueio, e cada avaliador tem uma observação para cada instrutor. O teste determinará se há diferenças entre os valores para o Instrutor, levando em consideração qualquer efeito consistente de um Avaliador.

Em outros casos, a variável de bloco pode ser a turma em que as classificações foram feitas ou a escola em que as classificações foram realizadas. Se você estava testando diferenças entre currículos ou outros tratamentos de ensino com diferentes instrutores, diferentes instrutores podem ser usados como blocos.

O teste de Friedman determina se há uma diferença sistemática nos valores da variável dependente entre os grupos.

12.2.3.1 Testes post-hoc

O resultado do teste de Friedman informa se existem diferenças entre os grupos, mas não informa quais grupos são diferentes de outros grupos. Para determinar quais grupos são diferentes dos outros, é possível realizar testes post-hoc.

12.2.3.2 Dados apropriados

Dados organizados em um design de bloco completo não replicado
A variável dependente é ordinal, discreta ou contínua
A variável independente de tratamento ou grupo é categórica com dois ou mais níveis. Ou seja, dois ou mais grupos.
Variável de bloqueio é categórica com dois ou mais níveis.
Os blocos são independentes um do outro e não têm interação com tratamentos.

12.2.3.3 Hipóteses

Hipótese nula: as distribuições (sejam elas quais forem) são as mesmas para cada grupo nos blocos. Hipótese alternativa: As distribuições para cada grupo entre os blocos são diferentes.

12.2.3.4 Interpretação

Resultados significativos podem ser relatados como “Houve uma diferença significativa nos valores da variável resposta entre os grupos”.

12.2.3.5 Outras anotações e testes alternativos

O teste Quade é usado para os mesmos tipos de dados e hipóteses, mas pode ser mais poderoso em alguns casos. Foi sugerido que o teste de Friedman pode ser preferível quando há um número maior de grupos (cinco ou mais), enquanto o Quade é preferível para menos grupos.

12.2.3.6 Exemplo do teste de Friedman

#-------------------------------------------------------------

Entrada =("
 Instrutor        Avaliador  Nota
 'Bob Belcher'        a      4
 'Bob Belcher'        b      5
 'Bob Belcher'        c      4
 'Bob Belcher'        d      6
 'Bob Belcher'        e      6
 'Bob Belcher'        f      6
 'Bob Belcher'        g     10
 'Bob Belcher'        h      6
 'Linda Belcher'      a      8
 'Linda Belcher'      b      6
 'Linda Belcher'      c      8
 'Linda Belcher'      d      8
 'Linda Belcher'      e      8
 'Linda Belcher'      f      7
 'Linda Belcher'      g     10
 'Linda Belcher'      h      9
 'Tina Belcher'       a      7
 'Tina Belcher'       b      5
 'Tina Belcher'       c      7
 'Tina Belcher'       d      8
 'Tina Belcher'       e      8
 'Tina Belcher'       f      9
 'Tina Belcher'       g     10
 'Tina Belcher'       h      9
 'Gene Belcher'       a      6
 'Gene Belcher'       b      4
 'Gene Belcher'       c      5
 'Gene Belcher'       d      5
 'Gene Belcher'       e      6
 'Gene Belcher'       f      6
 'Gene Belcher'       g      5
 'Gene Belcher'       h      5
 'Louise Belcher'     a      8
 'Louise Belcher'     b      7
 'Louise Belcher'     c      8
 'Louise Belcher'     d      8
 'Louise Belcher'     e      9
 'Louise Belcher'     f      9
 'Louise Belcher'     g      8
 'Louise Belcher'     h     10            
")

Dados = read.table(textConnection(Entrada),header=TRUE)

Dados$Nota_cat = as.factor(Dados$Nota)

### Verifique os dados
str(Dados)

## 'data.frame':    40 obs. of  4 variables:
##  $ Instrutor: Factor w/ 5 levels "Bob Belcher",..: 1 1 1 1 1 1 1 1 3 3 ...
##  $ Avaliador: Factor w/ 8 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 1 2 ...
##  $ Nota     : int  4 5 4 6 6 6 10 6 8 6 ...
##  $ Nota_cat : Factor w/ 7 levels "4","5","6","7",..: 1 2 1 3 3 3 7 3 5 3 ...

summary(Dados)

##           Instrutor   Avaliador       Nota        Nota_cat
##  Bob Belcher   :8   a      : 5   Min.   : 4.000   4 : 3   
##  Gene Belcher  :8   b      : 5   1st Qu.: 6.000   5 : 6   
##  Linda Belcher :8   c      : 5   Median : 7.000   6 : 8   
##  Louise Belcher:8   d      : 5   Mean   : 7.075   7 : 4   
##  Tina Belcher  :8   e      : 5   3rd Qu.: 8.000   8 :10   
##                     f      : 5   Max.   :10.000   9 : 5   
##                     (Other):10                    10: 4

### Remova objetos desnecessários
rm(Entrada)

### Teste de Friedman
friedman.test(Nota ~ Instrutor | Avaliador,
              data = Dados)

## 
##  Friedman rank sum test
## 
## data:  Nota and Instrutor and Avaliador
## Friedman chi-squared = 23.139, df = 4, p-value = 0.0001188

# Comparações pareadas usando o teste de Conover para um projeto de bloco completo balanceado
library(PMCMR)
PFCT <- posthoc.friedman.conover.test(y    = Dados$Nota,
                                   groups = Dados$Instrutor,
                                   blocks = Dados$Avaliador,
                                   p.adjust.method="fdr")
# P-valor para comparações pareadas 
PFCT

## 
##  Pairwise comparisons using Conover's test for a two-way 
##                     balanced complete block design 
## 
## data:  Dados$Nota , Dados$Instrutor and Dados$Avaliador 
## 
##                Bob Belcher Gene Belcher Linda Belcher Louise Belcher
## Gene Belcher   0.17328     -            -             -             
## Linda Belcher  0.00002796  0.00000117   -             -             
## Louise Belcher 0.00000190  0.00000011   0.27303       -             
## Tina Belcher   0.00037     0.00000877   0.31821       0.05154       
## 
## P value adjustment method: fdr

12.2.4 ANOVA de transformação de postos alinhados

Esse seguimento é uma tentativa de tradução do livro Mangiafico (2015). Se você quiser ler o documento original, clique aqui.

A ANOVA de transformação de postos alinhados - ART-ANOVA (Aligned Ranks Transformation ANOVA) é uma abordagem não paramétrica que permite múltiplas variáveis independentes, interações e medidas repetidas.

Neste modelo a variável dependente precisa ter uma natureza quantitativa. Ou seja,no processo, os dados ordinais precisariam ser tratados como numéricos. O pacote ARTool torna o uso dessa abordagem no R relativamente fácil.

Algumas notas sobre o uso do ARTool:
• Todas as variáveis independentes devem ser nominais.
• Todas as interações de variáveis independentes fixas precisam ser incluídas no modelo
• Comparações post-hoc podem ser realizadas para os efeitos principais.
• Para efeitos de interações, comparações post-hoc podem ser realizadas para modelos com duas variáveis independentes. • Para modelos de efeitos fixos, o eta-quadrado pode ser calculado como um tamanho de efeito.

#-------------------------------------------------------------

### Banco de dados
Location = c(rep("Olympia" , 6), rep("Ventura", 6),
             rep("Northampton", 6), rep("Burlington", 6))
Tribe  = c(rep(c("Jedi", "Sith"), 12))
Midichlorians = c(10,  4, 12,  5, 15,  4, 15,  9, 15, 11, 18, 12,
                   8, 13,  8, 15, 10, 17, 22, 22, 20, 22, 20, 25)
Dados <- data.frame(Tribe, Location, Midichlorians)
str(Dados)

## 'data.frame':    24 obs. of  3 variables:
##  $ Tribe        : Factor w/ 2 levels "Jedi","Sith": 1 2 1 2 1 2 1 2 1 2 ...
##  $ Location     : Factor w/ 4 levels "Burlington","Northampton",..: 3 3 3 3 3 3 4 4 4 4 ...
##  $ Midichlorians: num  10 4 12 5 15 4 15 9 15 11 ...

### Remova objetos desnecessários
remove(Location,Tribe,Midichlorians)

### Aligned ranks anova
library(ARTool)
modelo <- art(Midichlorians ~ Tribe + Location + Tribe:Location,
                data = Dados)

### Art ANOVA
anova(modelo)

## Analysis of Variance of Aligned Rank Transformed Data
## 
## Table Type: Anova Table (Type III tests) 
## Model: No Repeated Measures (lm)
## Response: art(Midichlorians)
## 
##                  Df Df.res F value        Pr(>F)    
## 1 Tribe           1     16  3.0606      0.099364   .
## 2 Location        3     16 34.6201 0.00000031598 ***
## 3 Tribe:Location  3     16 29.9354 0.00000084929 ***
## ---
## Signif. codes:   0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

12.2.4.1 Comparações post-hoc para efeitos principais

As comparações post-hoc para efeitos principais podem ser tratadas pelo pacote emmeans da maneira usual, exceto que a função artlm deve ser usada para ajustar primeiro um modelo que pode ser passado para emmeans. Os valores estimados na saída emmeans devem ser ignorados.

#-------------------------------------------------------------

library(emmeans)
modelo.lm = artlm(modelo, "Location")
marginal = emmeans(modelo.lm,~ Location)
pairs(marginal,adjust = "tukey")

##  contrast                 estimate   SE df t.ratio p.value
##  Burlington - Northampton    10.83 1.78 16  6.075  0.0001 
##  Burlington - Olympia        17.83 1.78 16 10.000  <.0001 
##  Burlington - Ventura         7.33 1.78 16  4.112  0.0041 
##  Northampton - Olympia        7.00 1.78 16  3.925  0.0060 
##  Northampton - Ventura       -3.50 1.78 16 -1.963  0.2426 
##  Olympia - Ventura          -10.50 1.78 16 -5.888  0.0001 
## 
## Results are averaged over the levels of: Tribe 
## P value adjustment: tukey method for comparing a family of 4 estimates

#Comparações post-hoc para interações
#Os valores estimados na saída emmeans devem ser ignorados.

modelo.int = artlm(modelo, "Tribe:Location")
marginal = emmeans(modelo.int, ~ Tribe:Location)
contrast(marginal, method="pairwise", adjust="none")

##  contrast                            estimate   SE df t.ratio p.value
##  Jedi,Burlington - Sith,Burlington     -6.500 2.68 16 -2.428  0.0273 
##  Jedi,Burlington - Jedi,Northampton     5.667 2.68 16  2.117  0.0503 
##  Jedi,Burlington - Sith,Northampton   -11.167 2.68 16 -4.171  0.0007 
##  Jedi,Burlington - Jedi,Olympia       -10.333 2.68 16 -3.860  0.0014 
##  Jedi,Burlington - Sith,Olympia         4.667 2.68 16  1.743  0.1005 
##  Jedi,Burlington - Jedi,Ventura        -8.667 2.68 16 -3.237  0.0052 
##  Jedi,Burlington - Sith,Ventura         1.000 2.68 16  0.374  0.7136 
##  Sith,Burlington - Jedi,Northampton    12.167 2.68 16  4.545  0.0003 
##  Sith,Burlington - Sith,Northampton    -4.667 2.68 16 -1.743  0.1005 
##  Sith,Burlington - Jedi,Olympia        -3.833 2.68 16 -1.432  0.1714 
##  Sith,Burlington - Sith,Olympia        11.167 2.68 16  4.171  0.0007 
##  Sith,Burlington - Jedi,Ventura        -2.167 2.68 16 -0.809  0.4302 
##  Sith,Burlington - Sith,Ventura         7.500 2.68 16  2.802  0.0128 
##  Jedi,Northampton - Sith,Northampton  -16.833 2.68 16 -6.288  <.0001 
##  Jedi,Northampton - Jedi,Olympia      -16.000 2.68 16 -5.977  <.0001 
##  Jedi,Northampton - Sith,Olympia       -1.000 2.68 16 -0.374  0.7136 
##  Jedi,Northampton - Jedi,Ventura      -14.333 2.68 16 -5.354  0.0001 
##  Jedi,Northampton - Sith,Ventura       -4.667 2.68 16 -1.743  0.1005 
##  Sith,Northampton - Jedi,Olympia        0.833 2.68 16  0.311  0.7596 
##  Sith,Northampton - Sith,Olympia       15.833 2.68 16  5.914  <.0001 
##  Sith,Northampton - Jedi,Ventura        2.500 2.68 16  0.934  0.3643 
##  Sith,Northampton - Sith,Ventura       12.167 2.68 16  4.545  0.0003 
##  Jedi,Olympia - Sith,Olympia           15.000 2.68 16  5.603  <.0001 
##  Jedi,Olympia - Jedi,Ventura            1.667 2.68 16  0.623  0.5423 
##  Jedi,Olympia - Sith,Ventura           11.333 2.68 16  4.233  0.0006 
##  Sith,Olympia - Jedi,Ventura          -13.333 2.68 16 -4.981  0.0001 
##  Sith,Olympia - Sith,Ventura           -3.667 2.68 16 -1.370  0.1897 
##  Jedi,Ventura - Sith,Ventura            9.667 2.68 16  3.611  0.0023

#Comparações post-hoc para outras interações
#Os valores estimados na saída emmeans devem ser ignorados.

modelo.diff = artlm(modelo, "Tribe:Location")
marginal = emmeans(modelo.diff, ~Tribe:Location)
contrast(marginal, method="pairwise", interaction=TRUE)

##  Tribe_pairwise Location_pairwise        estimate   SE df t.ratio p.value
##  Jedi - Sith    Burlington - Northampton    10.33 3.79 16  2.729  0.0148 
##  Jedi - Sith    Burlington - Olympia       -21.50 3.79 16 -5.679  <.0001 
##  Jedi - Sith    Burlington - Ventura       -16.17 3.79 16 -4.270  0.0006 
##  Jedi - Sith    Northampton - Olympia      -31.83 3.79 16 -8.408  <.0001 
##  Jedi - Sith    Northampton - Ventura      -26.50 3.79 16 -7.000  <.0001 
##  Jedi - Sith    Olympia - Ventura            5.33 3.79 16  1.409  0.1781

12.2.4.1.1 Eta quadrado parcial

O eta-quadrado parcial pode ser calculado como uma estatística de tamanho de efeito para a Art ANOVA.

12.2.4.1.2 Interpretação de eta-quadrado

A interpretação dos tamanhos dos efeitos varia necessariamente de acordo com a disciplina e as expectativas do experimento, mas, para estudos comportamentais, são seguidas as diretrizes propostas por Cohen (1988). Elas não devem ser consideradas universais.

            Small         Medium    Large

eta-squared 0.01–< 0.06 0.06–< 0.14 ≥0.14 Source: Cohen (1988).

#-------------------------------------------------------------
Resultado <- anova(modelo)

Resultado$eta.quadrado.parcial <- with(Resultado, `Sum Sq`/(`Sum Sq` + `Sum Sq.res`))

Resultado

## Analysis of Variance of Aligned Rank Transformed Data
## 
## Table Type: Anova Table (Type III tests) 
## Model: No Repeated Measures (lm)
## Response: art(Midichlorians)
## 
##                  Df Df.res F value        Pr(>F) eta.quadrado.parcial    
## 1 Tribe           1     16  3.0606      0.099364              0.16057   .
## 2 Location        3     16 34.6201 0.00000031598              0.86651 ***
## 3 Tribe:Location  3     16 29.9354 0.00000084929              0.84878 ***
## ---
## Signif. codes:   0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1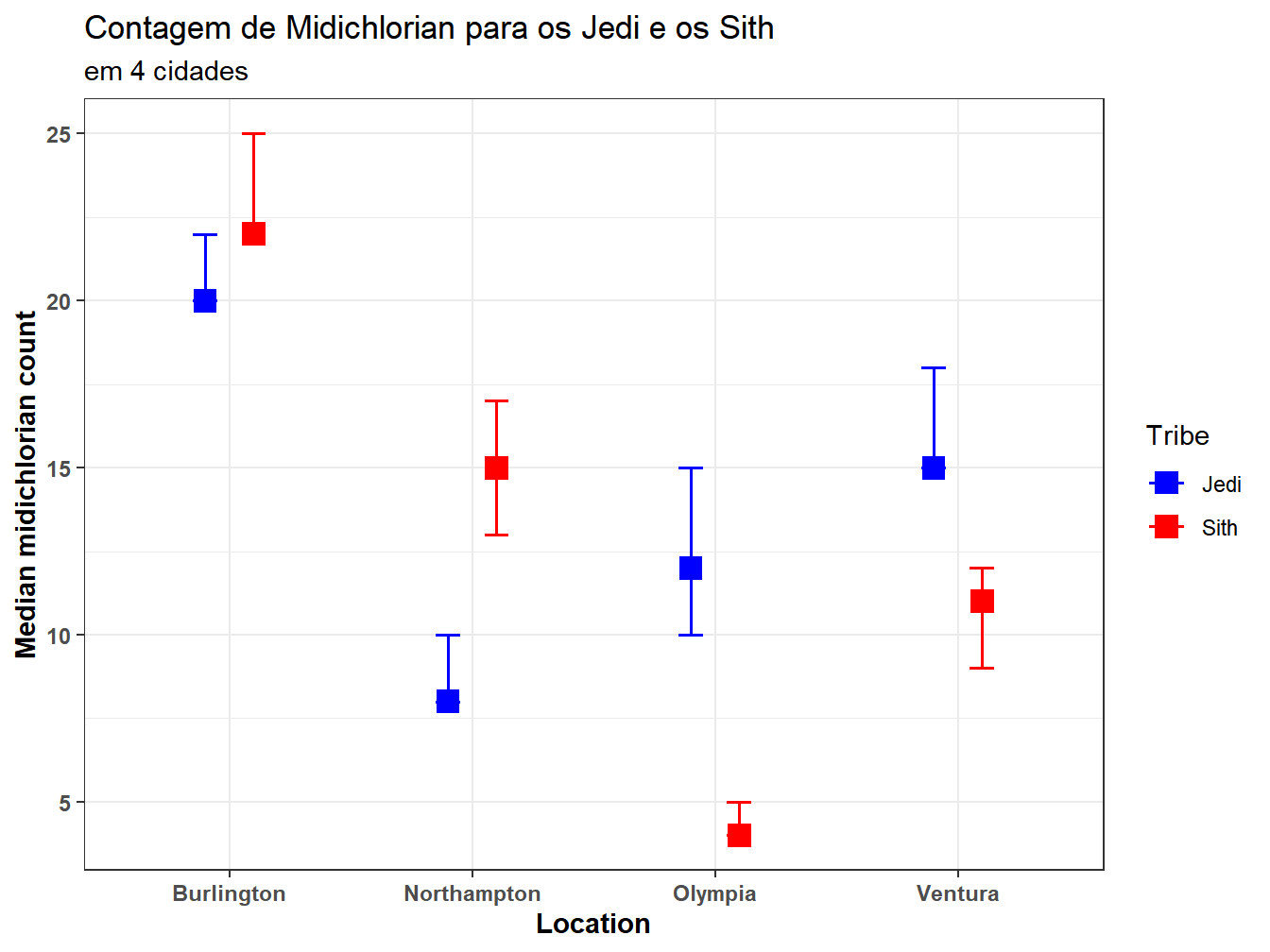

Referências - parte 1

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, 2nd Edition. Routledge.
Kay, M. 2019. Contrast tests with ART. cran.r-project.org/web/packages/ARTool/vignettes/art-contrasts.html.
Kay, M. 2019. Effect Sizes with ART. https://cran.r-project.org/web/packages/ARTool/vignettes/art-effect-size.html.
Kay, M. 2019. Package ‘ARTool’. cran.r-project.org/web/packages/ARTool/ARTool.pdf.
Wobbrock, J. O., Findlater, L., Gergle, D., & Higgins, J. J. 2011. The aligned rank transform for nonparametric factorial analyses using only anova procedures. In Conference on Human Factors in Computing Systems (pp. 143–146). faculty.washington.edu/wobbrock/pubs/chi-11.06.pdf.
Wobbrock, J. O., Findlater, L., Gergle, D., Higgins, J. J., & Kay, M. 2018. ARTool: Align-and-rank data for a nonparametric ANOVA. University of Washington. depts.washington.edu/madlab/proj/art/index.html.

Referências

Mangiafico, S. S. 2015. An R Companion for the Handbook of Biological Statistics, Version 1.3.2. https://rcompanion.org/rcompanion/.

Montgomery, Douglas. 2019. Design and Analysis of Experiments. Editora John Wiley; Sons. https://www.amazon.com/Design-Analysis-Experiments-Douglas-Montgomery/dp/1118146921.