Capítulo 11 Associação entre duas variáveis qualitativas

11.1 Teste Qui-Quadrado

O teste do Qui-Quadrado para independência compara duas variáveis qualitativas em uma tabela de contingência para verificar se elas estão relacionadas. O Teste Qui-Quadrado mede como os valores esperados se comparam aos dados reais observados.

11.1.0.1 Dados apropriados

Variáveis categóricas
Pelo menos cinco observações em cada celula da tabela de contigência (contagem esperada em cada celula)

11.1.0.2 Hipóteses

Hipótese nula: Não existe associação entre as variáveis
Hipótese alternativa: Existe associação entre as variáveis

11.1.0.3 Interpretação

Resultados significativos podem ser relatados como “há associação entre as duas variáveis”.

### Tabela para o teste
M <- as.table(rbind(c(762, 327, 468), c(484, 239, 477)))
### Rótulos para tabela
dimnames(M) <- list(sexo = c("Feminino", "Masculino"),
                    partido = c("PT","Outro partido", "PSDB"))

#### Gráfico  
library("gplots")
balloonplot(t(M), main ="Exemplo do Agresti", xlab ="", ylab="",
            label = FALSE, show.margins = FALSE)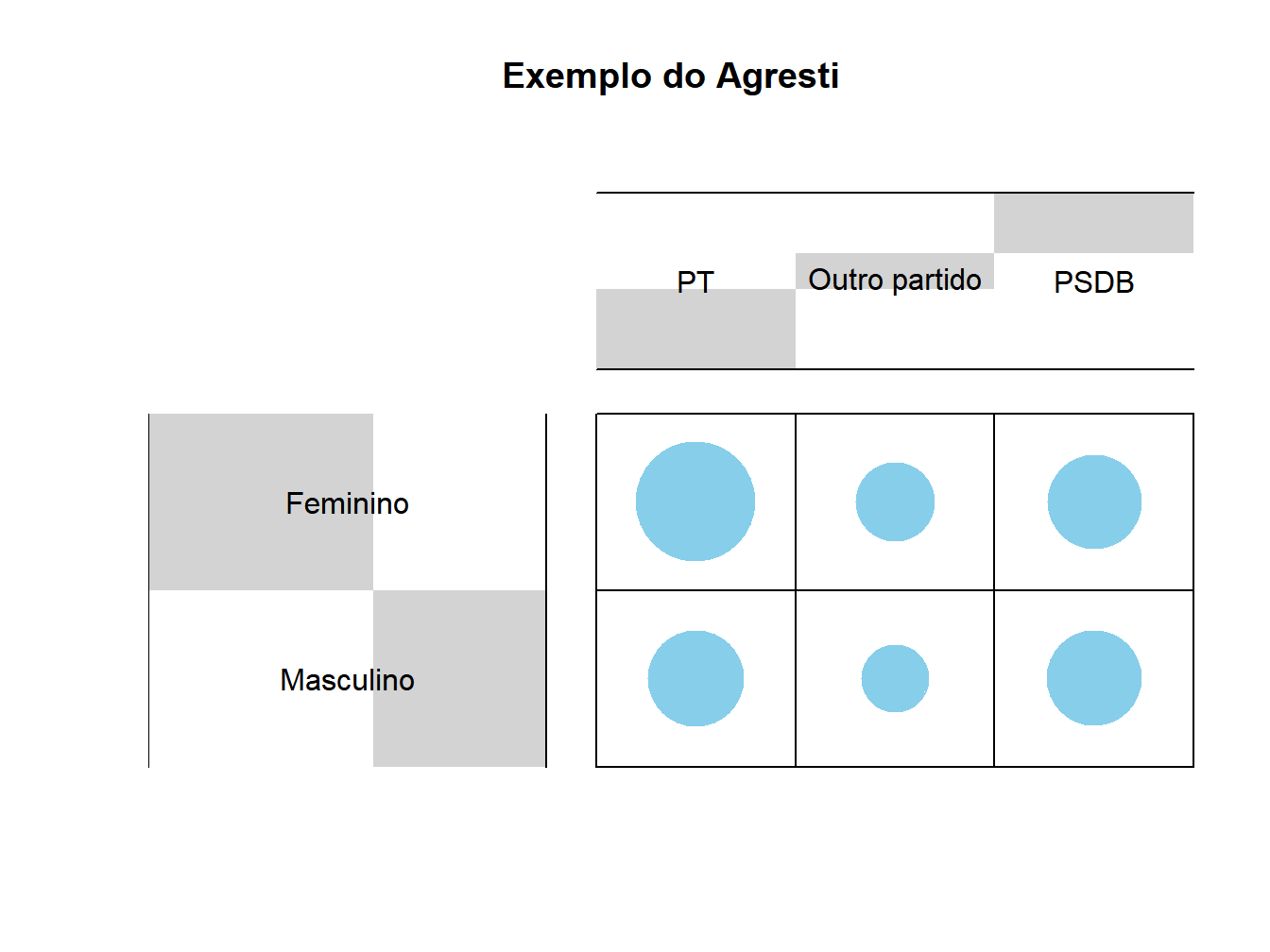

Figura 11.1: Teste Qui-quadrado

#### Resumo dos dados
M

##            partido
## sexo         PT Outro partido PSDB
##   Feminino  762           327  468
##   Masculino 484           239  477

#### Teste Qui-Quadrado
Xsq <- chisq.test(M)  
Xsq

## 
##  Pearson's Chi-squared test
## 
## data:  M
## X-squared = 30.07, df = 2, p-value = 0.0000002954

#### Valores observados (mesmo valor que a tabela M)
Xsq$observed

##            partido
## sexo         PT Outro partido PSDB
##   Feminino  762           327  468
##   Masculino 484           239  477

#### Valores esperados sob a hipótese nula
Xsq$expected

##            partido
## sexo              PT Outro partido     PSDB
##   Feminino  703.6714      319.6453 533.6834
##   Masculino 542.3286      246.3547 411.3166

# Devem ser maiores que cinco 
# (se tiver uma célula menor que cinco, você deve usar o teste exato de fisher)

Como todos os valores esperados são maiores que cinco, o teste Qui-Quadrado é adequado. O P-valor é menor que 0,05, logo, concluimos que existe associação entre as duas variáveis qualitativas. Em outras palavras, há prefência dos sexos pelos partidos políticos.

11.1.0.4 Limitação do teste qui-quadrado

O teste qui-quadrado pode ser usado apenas com números. Eles não podem ser usados para porcentagens, proporções, médias ou outras estatísticas. Assim, se você tiver 10% de 200 pessoas, precisará convertê-lo em um número (20) antes de poder executar o teste.

Referências do teste qui-quadrado Assumptions of the Chi-square The chi-square test of independence

11.2 Teste Exato de Fisher

11.2.0.1 Dados apropriados

Variáveis categóricas com dois níveis (exemplo: feminino/masculino)
Qualquer contagem em cada celula

11.2.0.2 Hipóteses

Hipótese nula: Não existe associação entre as variáveis
Hipótese alternativa: Existe associação entre as variáveis

11.2.0.3 Interpretação

Mesma interpretação do teste qui-quadrado. O teste exato de Fisher é interpretado da mesma forma que o teste qui-quadrado.

11.2.0.4 Exemplo do teste exato de Fisher

Um exemplo interessante de como podemos devenvolver testes para tudo é apresentado em (Agresti 2002). Uma ótima referência para esse experimento é o livro de Salsburg (2009).

O gosto do chá muda de acordo com a ordem em que as ervas e o leite são colocados? Uma britânica diz ser uma especialista em chá. Ela afirmou ser capaz de distinguir se leite ou chá foi adicionado à xícara primeiro. Leite sobre o chá ou chá sobre o leite.

Vamos construir um experimento para verificar isso? Para testar, ela recebeu 8 xícaras de chá, das quais quatro o chá foi adicionado antes do leite.

A hipótese nula é a de que não há associação entre a verdadeira ordem dos ingredientes e a opinião da mulher, a hipótese alternativa de que existe uma associação positiva (que a razão de chances é maior que 1).

### Tabela para o teste
resultado_xicaras <-matrix(c(3, 1, 1, 3),
       nrow = 2, dimnames = 
         list(opiniao = c("Leite", "Chá"),
              verdadeiro_result = c("Leite", "Chá")))

resultado_xicaras

##        verdadeiro_result
## opiniao Leite Chá
##   Leite     3   1
##   Chá       1   3

#### Teste Exato de Fisher
Teste_fisher <- fisher.test(resultado_xicaras, alternative = "greater")
Teste_fisher

## 
##  Fisher's Exact Test for Count Data
## 
## data:  resultado_xicaras
## p-value = 0.2429
## alternative hypothesis: true odds ratio is greater than 1
## 95 percent confidence interval:
##  0.3135693       Inf
## sample estimates:
## odds ratio 
##   6.408309

11.2.0.5 Teste exato de Fisher com mais de duas categorias

Se você tiver tabelas maiores que 2 por 2 (mais de duas categorias em uma das variáveis), socê pode usar uma aproximação híbrida.

### Tabela para o teste
Tabela <- as.table(rbind(c(2,3,10,6,1), c(1,6,7,14,12)))

### Rótulos para tabela
dimnames(Tabela) <- list(sexo = c("Feminino", "Masculino"),
                    likert = c("Concordo Totalmente","Concordo",
                               "Nem concordo nem discordo",
                               "Discordo", "Discordo Totalmente"))
Tabela

##            likert
## sexo        Concordo Totalmente Concordo Nem concordo nem discordo Discordo
##   Feminino                    2        3                        10        6
##   Masculino                   1        6                         7       14
##            likert
## sexo        Discordo Totalmente
##   Feminino                    1
##   Masculino                  12

Teste_fisher_hybrid <- fisher.test(Tabela,  hybrid=TRUE)
Teste_fisher_hybrid

## 
##  Fisher's Exact Test for Count Data hybrid using asym.chisq. iff
##  (exp=5, perc=80, Emin=1)
## 
## data:  Tabela
## p-value = 0.03019
## alternative hypothesis: two.sided

Referências

Agresti, Alan. 2002. Categorical Data Analysis, Second Edition. New York: Editora Wiley.

Salsburg, David. 2009. Uma Senhora Toma Chá. Como a Estatística Revolucionou a Ciência No Século Xx. Editora Zahar. https://zahar.com.br/livro/uma-senhora-toma-cha.