Capítulo 8 Homogeneidade de variâncias
8.1 Teste de Bartlett
8.1.0.1 Por que usar?
O teste de Bartlett é usado para verificar se as amostras têm homogeneidade de variâncias (variâncias iguais). A avaliação do pressuposto de homogeneidade de variâncias é exigida pela maioria dos procedimentos estatísticos. Muitos testes estatísticos assumem que as variâncias são iguais entre grupos. O teste de Bartlett pode ser usado para verificar essa pressuposto. É realizado com a função bartlett.test.
8.1.0.2 Pressupostos
O teste assume que as observações são independentes.
8.1.0.3 Dados apropriados
• A variável dependente é quantitativa. • A variável independente é qualitativa.
8.1.0.4 Hipóteses
Hipótese nula: \(\sigma^{2}_1 = \sigma^{2}_2 = \sigma^{2}_3 = ... = \sigma^{2}_k\) (as variâncias são iguais)
Hipótese alternativa: \(\sigma^{2}_i \neq \sigma^{2}_j\) (As variâncias são desiguais para pelo menos dois grupos)
8.1.0.5 Interpretação
Resultados significativos podem ser relatados como “os grupos têm variâncias desiguais”, “os dados são heterocedásticos”, "a variável resposta viola o pressuposto de homogeneidade de variâncias.
8.1.0.6 Exemplo de teste de Bartlett
Este exemplo apresenta os dados de uma amostra de 32 carros.
Esse teste responde à pergunta: “A variância da variável Km/L (quantitativa) é igual para os dois grupos de carros (gasolina/álcool)?”
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
"Amperagem_circ_eletrico","Peso","RPM",
"Tipodecombustivel","TipodeMarcha",
"NumdeMarchas","NumdeValvulas")
CARROS$Tipodecombustivel<-as.factor(CARROS$Tipodecombustivel)
levels(CARROS$Tipodecombustivel) <- c('Gasolina','Álcool')
### Verifique os dados
str(CARROS$Kmporlitro)## num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...## Factor w/ 2 levels "Gasolina","Álcool": 1 1 2 2 1 2 1 2 2 2 ...### Remova objetos desnecessários
remove(mtcars)
#### Resumo dos dados por grupo de combustivel
library(psych)Attaching package: ‘psych’
The following objects are masked from ‘package:ggplot2’:
%+%, alpha##
## Descriptive statistics by group
## group: Gasolina
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 18 16.62 3.86 15.65 16.42 2.97 10.4 26 15.6 0.48 -0.05 0.91
## ------------------------------------------------------------
## group: Álcool
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 14 24.56 5.38 22.8 24.34 6 17.8 33.9 16.1 0.41 -1.4 1.44#### Box-plot por grupo de combustivel
boxplot(CARROS$Kmporlitro~CARROS$Tipodecombustivel,
horizontal = TRUE,col=c("skyblue","red"))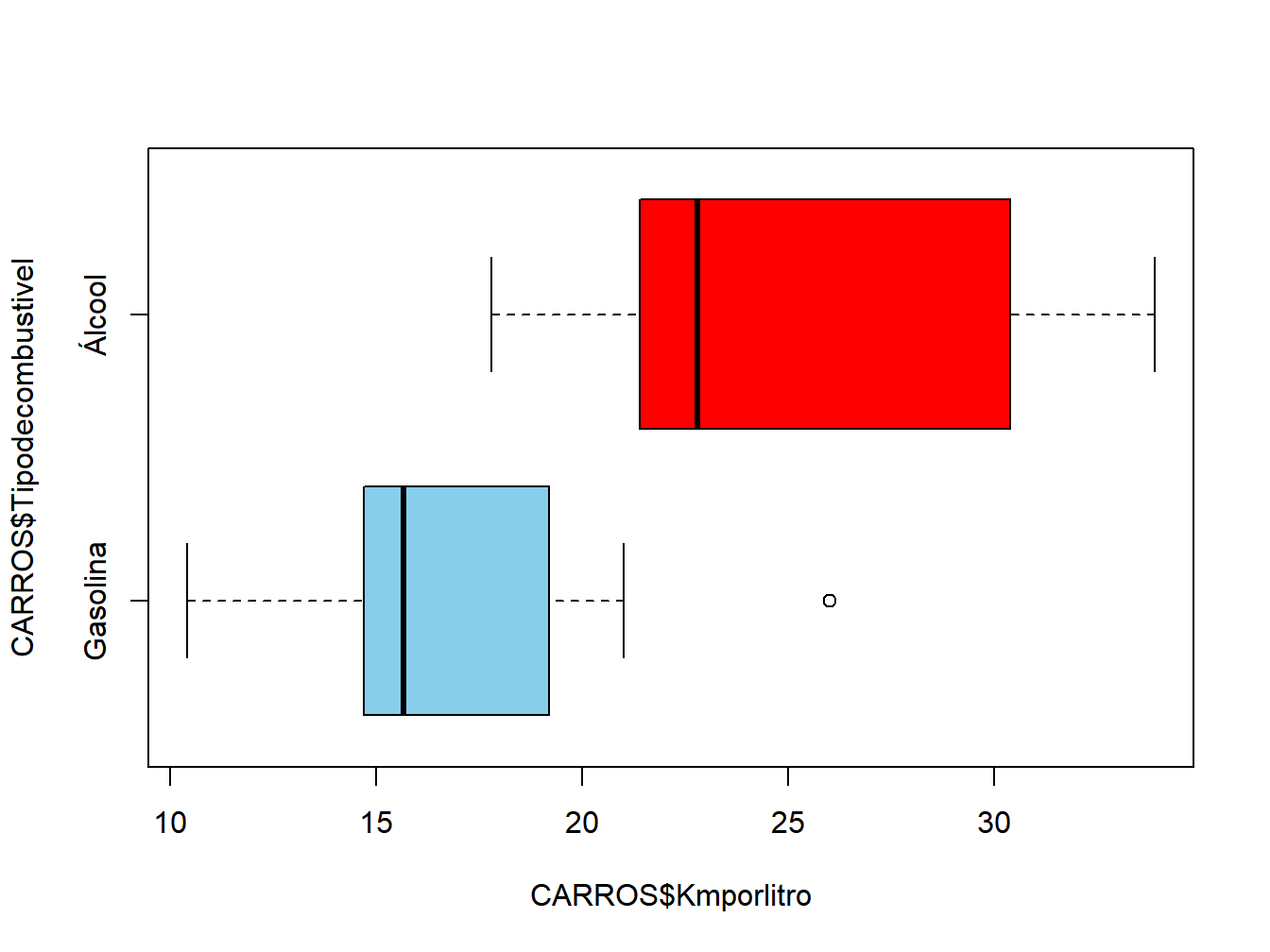
Figura 8.1: Teste
##
## Bartlett test of homogeneity of variances
##
## data: CARROS$Kmporlitro by CARROS$Tipodecombustivel
## Bartlett's K-squared = 1.5849, df = 1, p-value = 0.2081Falhamos em rejeitar a hipótese nula de homogeneidade de variâncias. Ou seja, os dois tipos de combustivel (Gasolina/Álcool) têm variâncias homogêneas para a variável Km/l.
8.1.0.7 Observação
Esse teste é equivalente ao Teste Breusch-Pagan de heterocedásticidade nos modelos lineares.
8.1.0.8 Limitação do teste
O teste de Bartlett é sensível a desvios da normalidade. Recomendo fazê-lo depois do teste de normalidade.
Se suas amostras são provenientes de uma distribuição que não é normal, o teste de Bartlett pode falhar. O teste de Levene é uma alternativa ao teste Bartlett, menos sensível a desvios da normalidade. Em outras palavras, se a distribuição não é normal, use o teste de levene.
8.1.0.9 Exemplo do Teste de Levene
Loading required package: carData
Attaching package: ‘car’
The following object is masked from ‘package:psych’:
logit## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 4.3041 0.0467 *
## 30
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1