Capítulo 7 Teste de Normalidade de Shapiro Wilk
7.0.0.1 Por que usar?
O Shapiro Wilk é um teste para aferir a normalidade dos dados (se a variável segue uma distribuição normal). A avaliação do pressuposto de normalidade é exigida pela maioria dos procedimentos estatísticos. A análise estatística paramétrica é um dos melhores exemplos para mostrar a importância de avaliar a suposição de normalidade.
A estatística paramétrica assume uma certa distribuição dos dados, geralmente a distribuição normal. Se a suposição de normalidade for violada, a interpretação, a inferência, e a conclusão a partir dos dados podem não ser confiáveis ou válidas.
Existem outros testes de normalidade (Jarque-Bera, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling). Recomendo o uso do Shapiro Wilk porque ele é geralmente poderoso, fácil de usar, e muitas pessoas estão familiarizadas com ele (diminuindo a necessidade de explicar em detalhes a abordagem se você o usar em um artigo). É realizado com a função shapiro.test.
7.0.0.2 Pressupostos
O teste assume que as observações são independentes.
7.0.0.3 Dados apropriados
• A variável dependente é quantitativa.
7.0.0.4 Hipóteses
Hipótese nula: os dados são normalmente distribuídos (os dados seguem uma distribuição normal).
Hipótese alternativa: os dados não são normalmente distribuídos (os dados não seguem uma distribuição normal).
7.0.0.5 Interpretação
Resultados significativos podem ser relatados como “os dados não seguem uma distribuição normal” ou como “a hipótese nula de que os dados são normalmente distribuídos foi rejeitada”.
7.0.0.6 Exemplo de teste de Shapiro Wilk
Este exemplo apresenta os dados de uma amostra de 32 carros.
Esse teste responde à pergunta: “A variável preço do carro segue uma distribuição normal?”
O teste de Shapiro Wilk é realizado com a função shapiro.test, que produz um p-valor para a hipótese. Primeiro, os dados são resumidos. Em seguida, são examinados usando gráficos histograma, QQ-plot. Esses gráficos ajudam a decidir se a distribuição é normal.
#-------------------------------------------------------------
#### Crie o banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
"Amperagem_circ_eletrico","Peso","RPM",
"Tipodecombustivel","TipodeMarcha",
"NumdeMarchas","NumdeValvulas")
### Verifique os dados
str(CARROS$Preco)## num [1:32] 160 160 108 258 360 ...## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 71.1 120.8 196.3 230.7 326.0 472.0#### Histograma
hist(CARROS$Preco, prob=TRUE, col="red",main = "Histograma do preço do carro")
lines(density(CARROS$Preco),lwd=3,col="blue") 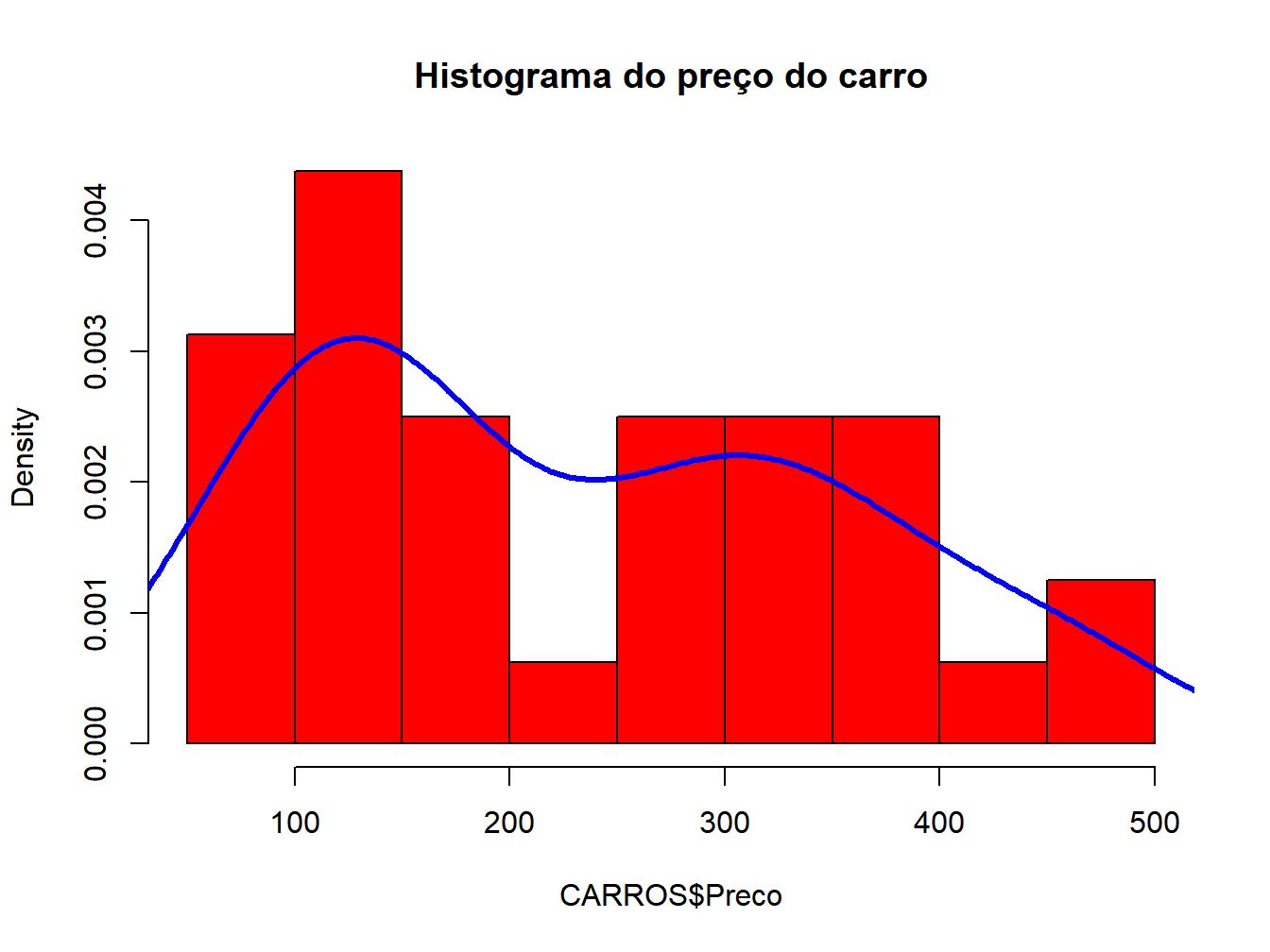
Figura 7.1: Teste de Shapiro Wilk
#### Grafico QQ-Plot
qqnorm(CARROS$Preco,xlab = "Quantis teóricos",
ylab = "Quantis observados",main = "QQ-plot")
qqline(CARROS$Preco, col = 2)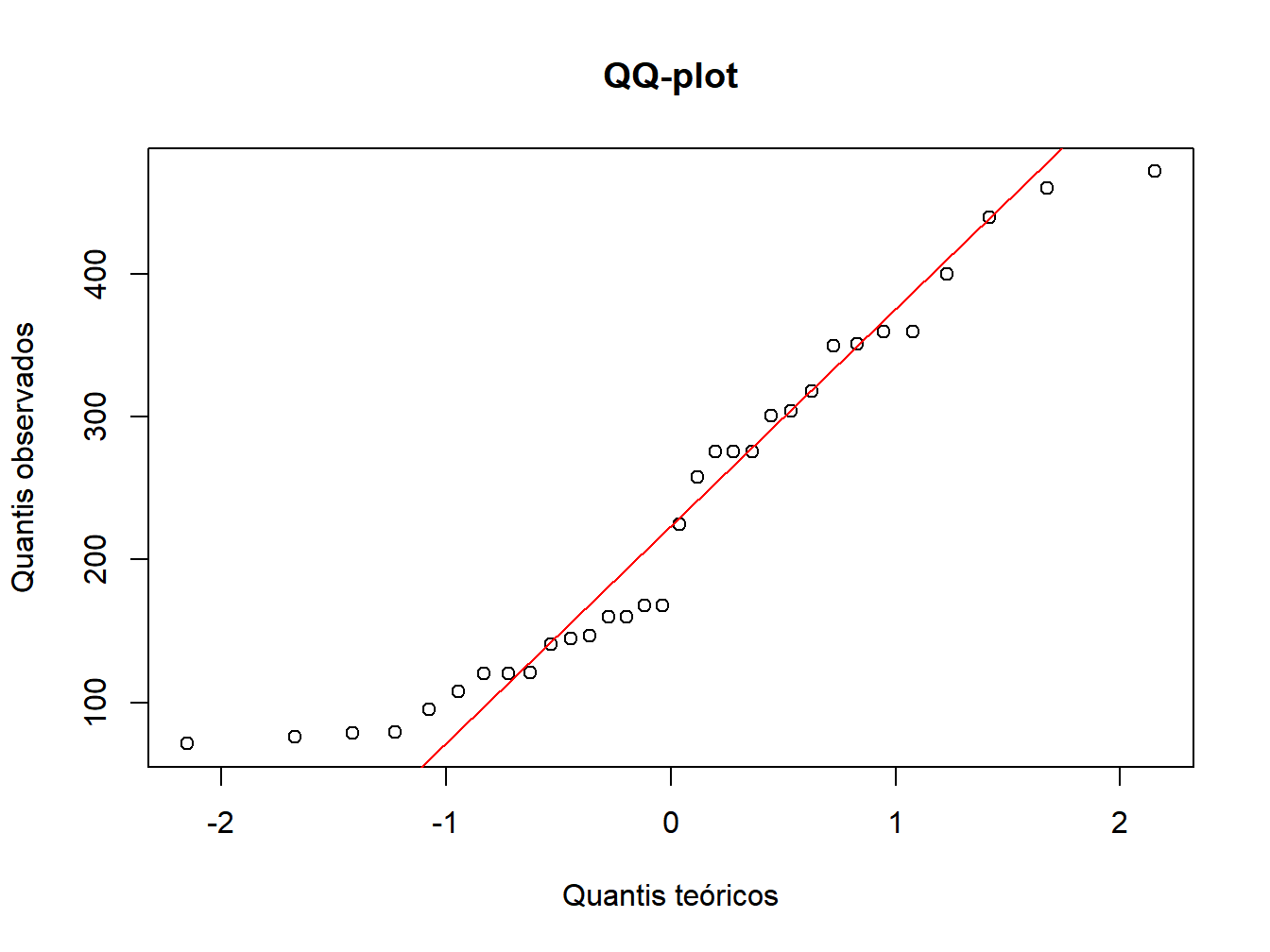
Figura 7.2: Teste de Shapiro Wilk
##
## Shapiro-Wilk normality test
##
## data: CARROS$Preco
## W = 0.92001, p-value = 0.02081O preço do carro não segue uma distribuição normal. Possivelmente, os outliers pode estar influenciando o resultado. Seria interessante deletar os outliers e refazer o teste.
7.0.0.7 Limitações do teste
Cumpre registrar uma limitação do teste de shapiro wilk. Se a sua base de dados tiver mais de 5.000 observações, o teste de Shapiro Wilk pode indicar que o seu banco de dados não segue uma distribuição normal mesmo quando ela tem essa distribuição.
Tem uma ótima discussão no stackexchange (em inglês). Ela pode ser encontrada aqui. Reproduzi parte da discussão abaixo.
#-------------------------------------------------------------
# semente para reproduzir o experimento
set.seed(981677672)
# procedimento para gerar 100 testes de
# Shapiro Wilk em cada distribuição normal.
# (com 10, 100,1.000,e 5.000 observações)
# a função rnorm gera um sorteio aleatório da distribuição normal
x <- replicate(100, {
c(shapiro.test(rnorm(10)+c(1,0,2,0,1))$p.value, #$
shapiro.test(rnorm(100)+c(1,0,2,0,1))$p.value,
shapiro.test(rnorm(1000)+c(1,0,2,0,1))$p.value,
shapiro.test(rnorm(5000)+c(1,0,2,0,1))$p.value)
}
)
rownames(x) <- c("n10","n100","n1000","n5000")
rowMeans(x<0.05) # a proporção de desvios significativos da normalidade## n10 n100 n1000 n5000
## 0.03 0.02 0.19 0.83A última linha verifica qual fração das simulações para cada o tamanho da amostra diverge significativamente da normalidade. Assim, em 83% dos casos, uma amostra de 5000 observações se desvia significativamente da normalidade de acordo com Shapiro-Wilk. No entanto, ao verificar os gráficos qq-plots, você nunca acreditaria no desvio da normalidade.