Capítulo 9 Outliers

Os valores extremos (outliers) nos dados podem distorcer as previsões. Os outliers também podem ser chamados de valores discrepantes. Acredito que é essencial entender o impacto deles nos seus testes de hipóteses.

Cabe ao melhor julgamento do análista decidir como fazer o tratamento de outliers.

Os outliers podem influenciar drasticamente as estimativas da variância. Além disso, se você está construindo um modelo, eles podem modificar a inclinação da Reta.

9.0.0.1 Exemplo da influência do outlier

Para entender melhor as implicações dos outliers, compararei o ajuste de um modelo de regressão linear simples no conjunto de dados de carros com e sem outliers.

Para distinguir claramente o efeito, vamos introduzir manualmente os outliers no conjunto de dados. Depois disso, vamos fazer uma regressão linear nos dois bancos de dados.

data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
                      "Amperagem_circ_eletrico","Peso","RPM",
                      "Tipodecombustivel","TipodeMarcha",
                      "NumdeMarchas","NumdeValvulas")
# Selecione somente o preço do carro e o HP (Horse Power - cavalos de potência)
CARROS<-CARROS[CARROS$HP<=334,c("Preco","HP")] # dados originais sem outliers

# Inserir outliers no banco de dados.
outliers_para_carros<-data.frame(Preco=c(319,590,500), 
                                 HP=c(590, 686, 690)) 

# novo banco de dados com outliers
CARROS_OUTLIERS<-rbind(CARROS, outliers_para_carros)

### Remova objetos desnecessários
remove(mtcars,outliers_para_carros)

### Graficos com outliers. 
par(mfrow=c(1, 2)) # grafico lado a lado

plot(CARROS_OUTLIERS$HP, CARROS_OUTLIERS$Preco, xlim=c(0, 700), 
     ylim=c(0, 600), main="Com outliers", xlab="cavalos de potência",
     ylab="Preço do carro", pch=19, col="red")
abline(lm(Preco~HP, data=CARROS_OUTLIERS), col="blue", lwd=3, lty=2)

### Graficos sem outliers (dados originais)
plot(CARROS$HP, CARROS$Preco, xlim=c(0, 700), ylim=c(0, 700),
     main="Sem outliers", xlab="cavalos de potência", 
     ylab="Preço do carro", pch=19, col="red") # um modelo melhor
abline(lm(Preco~HP, data=CARROS), col="blue", lwd=3, lty=2)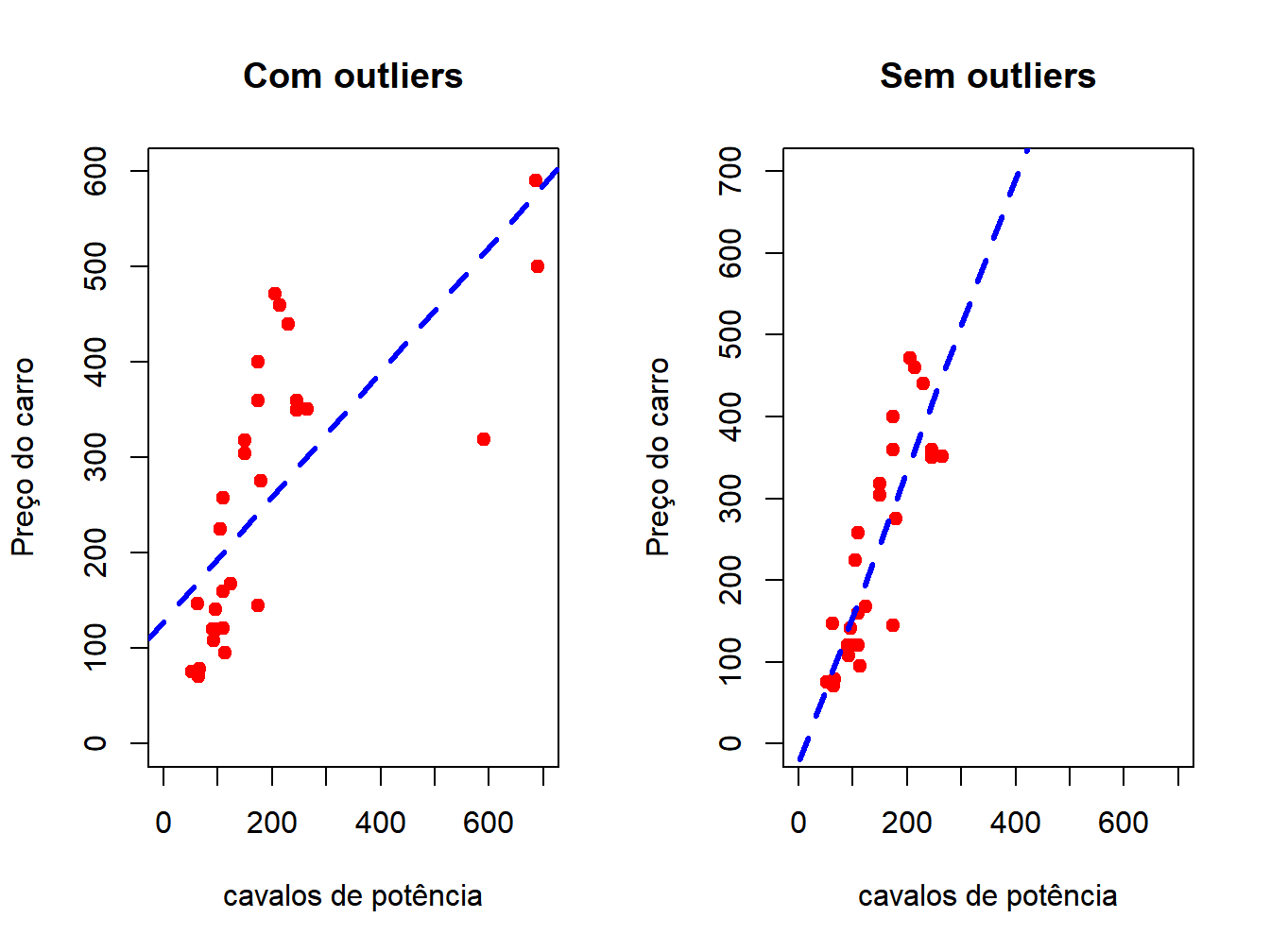

Figura 9.1: Impacto do outlier

9.0.0.2 Como encontrar os outliers?

Método básico

par(mfrow=c(1, 2))
valores_outliers <- boxplot.stats(CARROS_OUTLIERS$HP)$out  
boxplot(CARROS_OUTLIERS$HP, main="Cavalos de potência",ylim=c(0, 700))
mtext(paste("Outliers: os valores", paste(valores_outliers, collapse=", "),
            "da variável HP"), cex=0.8)
boxplot(CARROS$HP, main="Cavalos de potência", ylim=c(0, 700))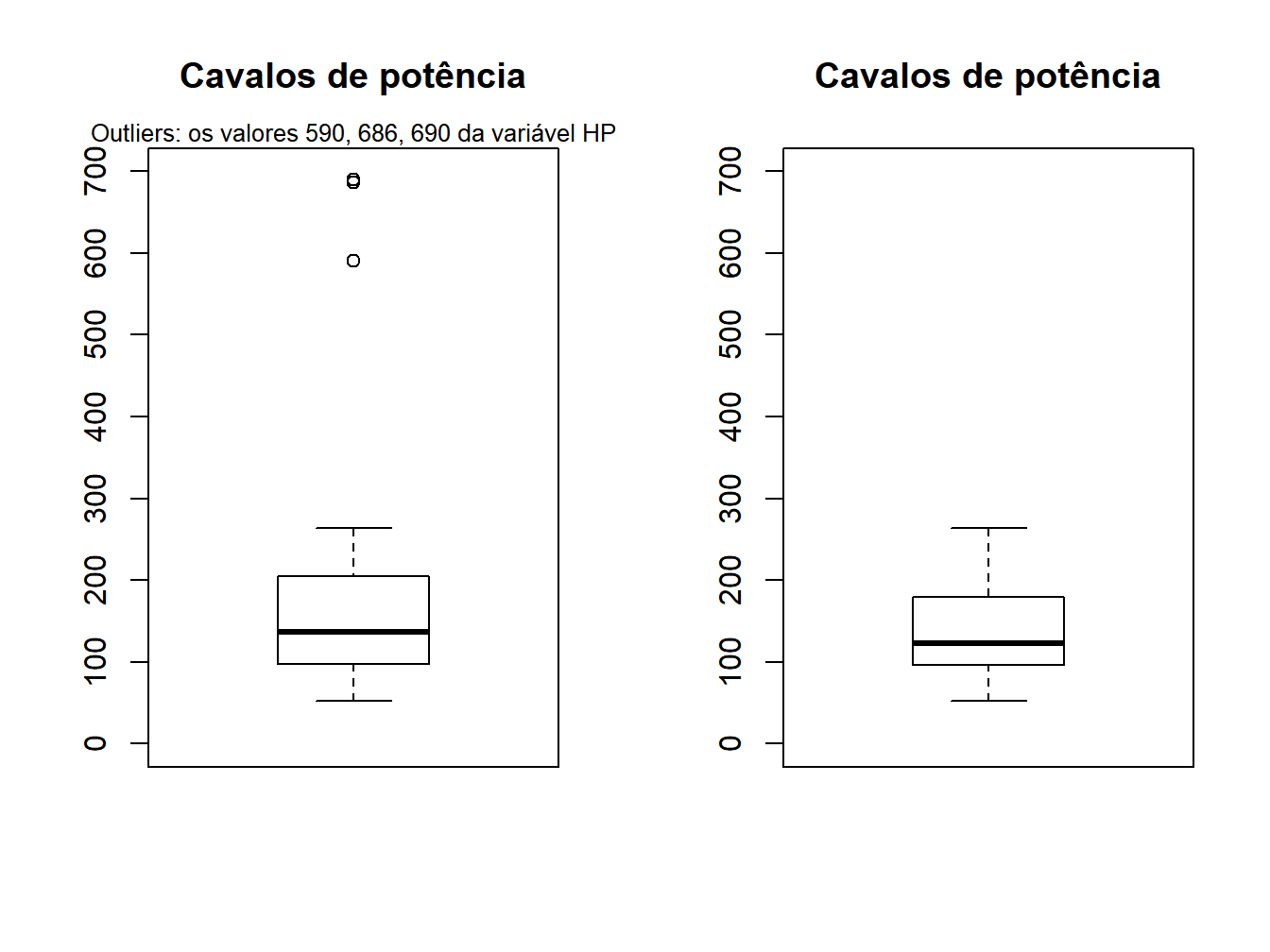

Figura 9.2: Outliers

par(mfrow=c(1, 1))

# Teste para Outliers e
# p-valor de Bonferonni para valores extremos
library(car)
modelo<-lm(CARROS$HP~CARROS$Preco)
outlierTest(modelo) 

## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##    rstudent unadjusted p-value Bonferroni p
## 29  2.62339           0.013932       0.4319

Ok. não temos outliers, mas podemos ter observações influêntes?

A distância de Cook

A distância de Cook mede a influência da observação sobre todos os valores ajustados.

plot(modelo, which=4)

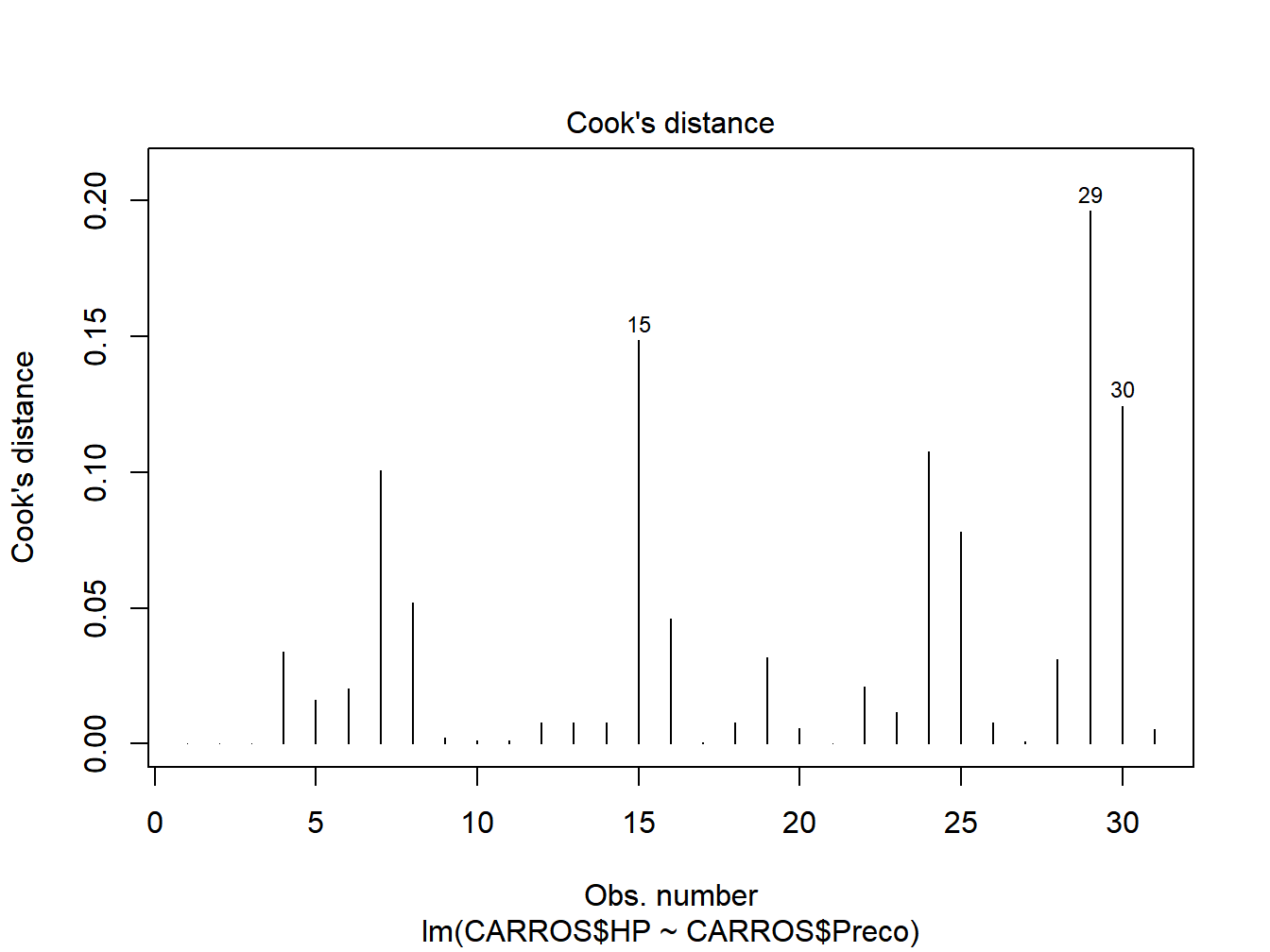
Figura 9.3: Outliers

# Influence Plot
influencePlot(modelo, id.method="identify", sub="o tamanho do círculo é 
              proporcional à distância de Cook")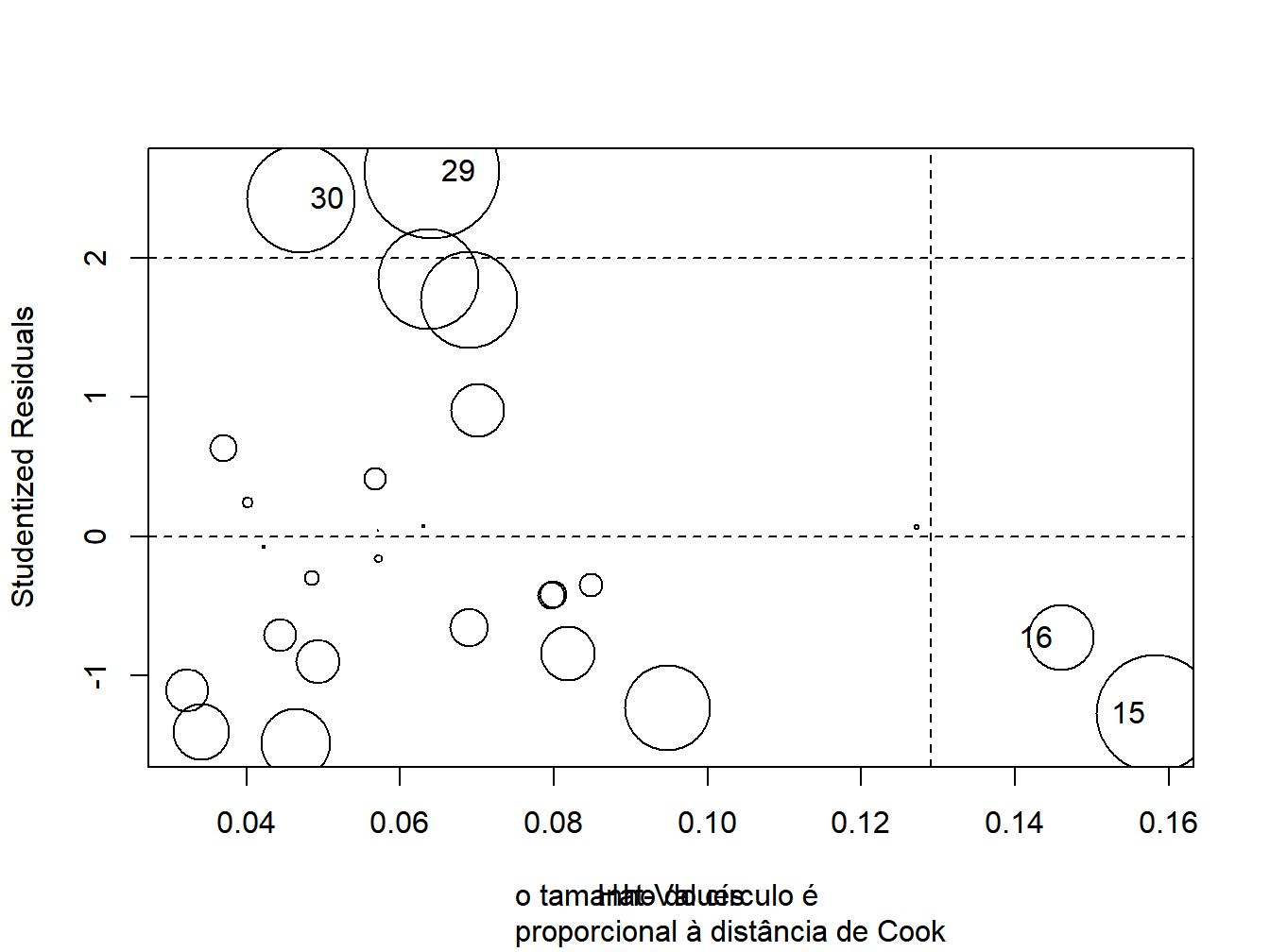

Figura 9.4: Outliers

##       StudRes        Hat     CookD
## 15 -1.2707146 0.15816753 0.1485416
## 16 -0.7275545 0.14606554 0.0460183
## 29  2.6233896 0.06413611 0.1960559
## 30  2.4263435 0.04704242 0.1243523

# vale a pena inverstigar as observações 15,16,29,e 30

Além da abordagem básica, os pacotes do R chamados de outliers e OutlierDetection podem ajuda-lo a decidir se uma observação é um outlier ou não

#--------------------------------------------------
# Teste
#--------------------------------------------------
library(outliers)
# teste se é um outlier
chisq.out.test(CARROS_OUTLIERS$Preco)

## 
##  chi-squared test for outlier
## 
## data:  CARROS_OUTLIERS$Preco
## X-squared = 5.7167, p-value = 0.0168
## alternative hypothesis: highest value 590 is an outlier

chisq.out.test(CARROS$Preco)

## 
##  chi-squared test for outlier
## 
## data:  CARROS$Preco
## X-squared = 3.7773, p-value = 0.05195
## alternative hypothesis: highest value 472 is an outlier

# remove o outlier do banco de dados
banco_sem_outliers<-rm.outlier(CARROS_OUTLIERS)
head(banco_sem_outliers)

##   Preco  HP
## 1   160 110
## 2   160 110
## 3   108  93
## 4   258 110
## 5   360 175
## 6   225 105

#--------------------------------------------------
# Grafico para mostrar os outliers
#--------------------------------------------------
library(OutlierDetection)
# Univariado - Outlier Detection
UnivariateOutlierDetection(CARROS_OUTLIERS$Preco)

## $`Outlier Observations`
## [1] 590 500
## 
## $`Location of Outlier`
## [1] 33 34
## 
## $`Scatter plot`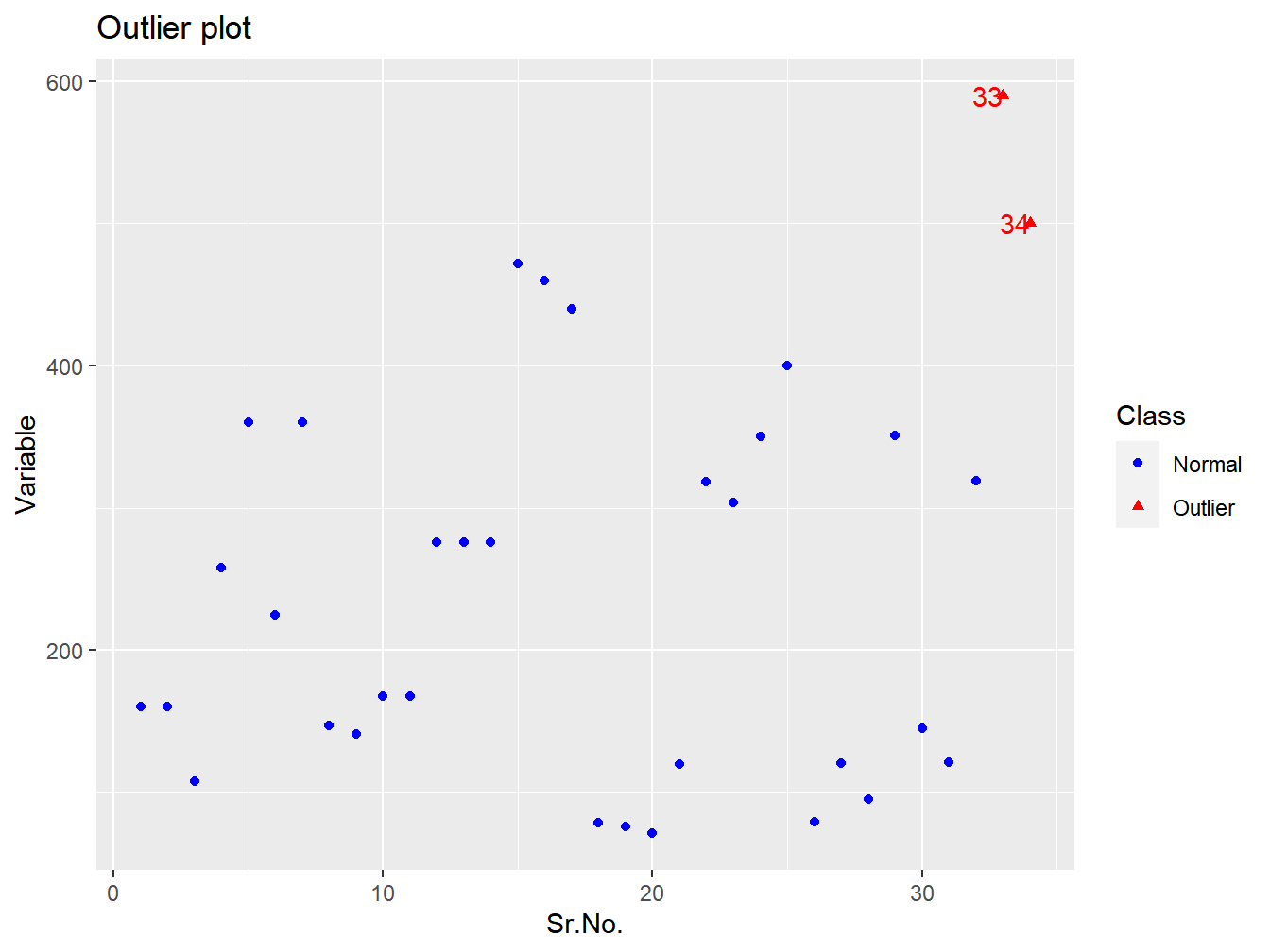

Figura 9.5: Outliers

UnivariateOutlierDetection(CARROS_OUTLIERS$HP)

## $`Outlier Observations`
## [1] 686 690
## 
## $`Location of Outlier`
## [1] 33 34
## 
## $`Scatter plot`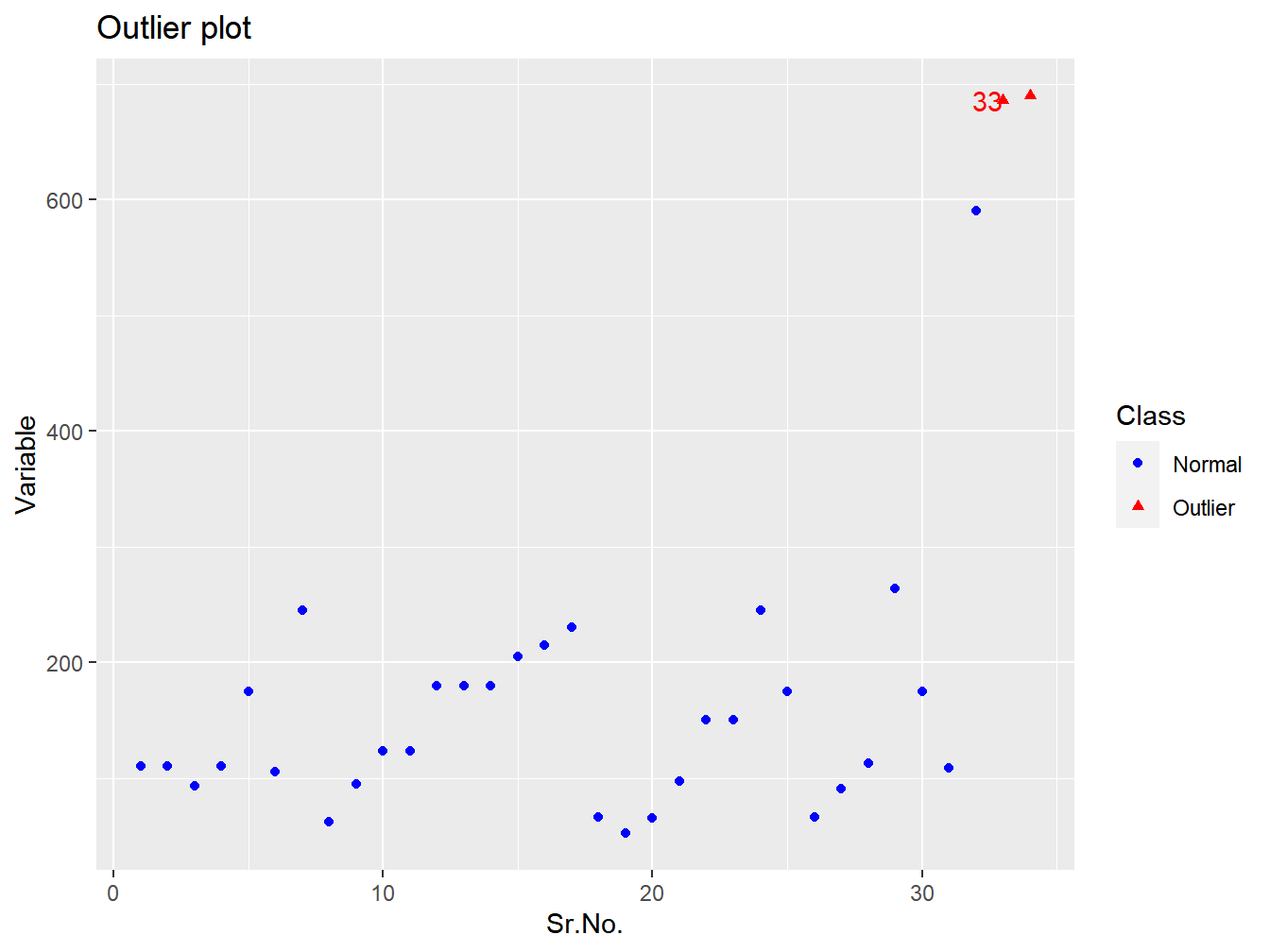

Figura 9.6: Outliers

# Bivariado - Outlier Detection
OutlierDetection(CARROS_OUTLIERS)

## $`Outlier Observations`
##   Preco  HP
## 1   319 590
## 2   590 686
## 3   500 690
## 
## $`Location of Outlier`
##  1  2  3 
## 32 33 34 
## 
## $`Scatter plot`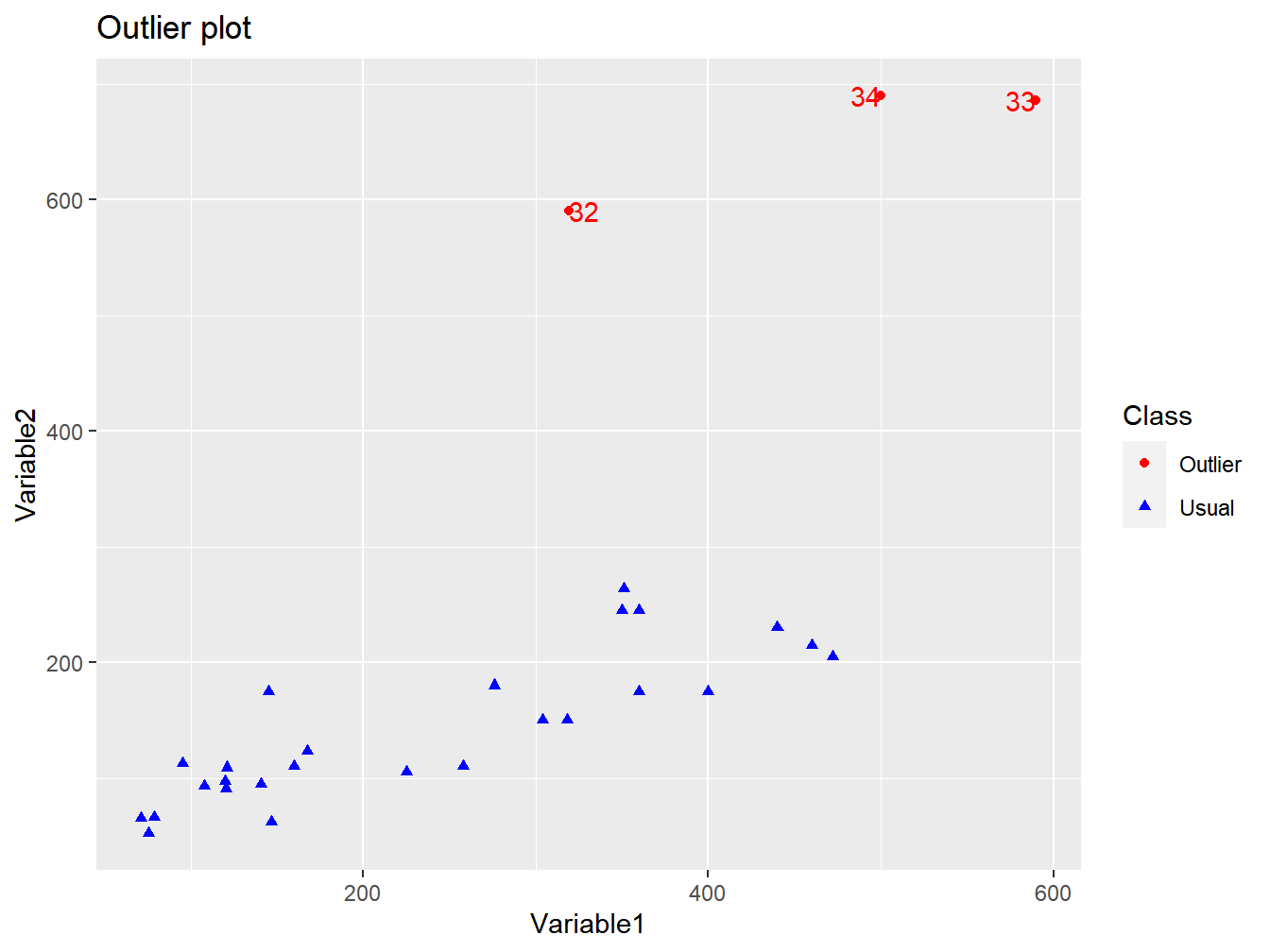

Figura 9.7: Outliers

Parece que o teste detectou que as observações 32,33, e 34 são outliers.