Capítulo 13 Associação entre duas variáveis quantitativas
13.1 Teste de correlação de pearson
O Teste de correlação de pearson faz a mensuração da associação linear entre duas variáveis quantitativas. Além disso, ele testa se essa correlaçao linear é significativa.
13.1.0.1 Dados apropriados
Utiliza-se este teste quando:
* Os dados seguem uma distribuição normal bi-variada.
13.1.0.2 Hipóteses
Hipótese nula: \(\rho=0\)
Hipótese alternativa: \(\rho \neq 0\)
13.1.0.3 Interpretação
Resultados significativos podem ser relatados como “A correlação é diferente de zero. As variáveis são correlacionadas”.
13.1.0.4 Exemplo
13.1.0.5 Exemplo do teste de correlação
Este exemplo apresenta os dados de uma amostra de 32 carros.
Esse teste responde à pergunta: “A variável Km/L (quantitativa) é correlacionada com o log do preço (quantitativa)”
#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
"Amperagem_circ_eletrico","Peso","RPM",
"Tipodecombustivel","TipodeMarcha",
"NumdeMarchas","NumdeValvulas")
CARROS$log_preco<-log(CARROS$Preco)
### Verifique os dados
str(CARROS$Kmporlitro)## num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...## num [1:32] 5.08 5.08 4.68 5.55 5.89 ...### Remova objetos desnecessários
remove(mtcars)
#### Resumo dos dados
library(ggplot2)
ggplot(CARROS) +
aes(x = Kmporlitro, y = log_preco) +
geom_point(size = 3L, colour = "#cb181d") +
theme_minimal()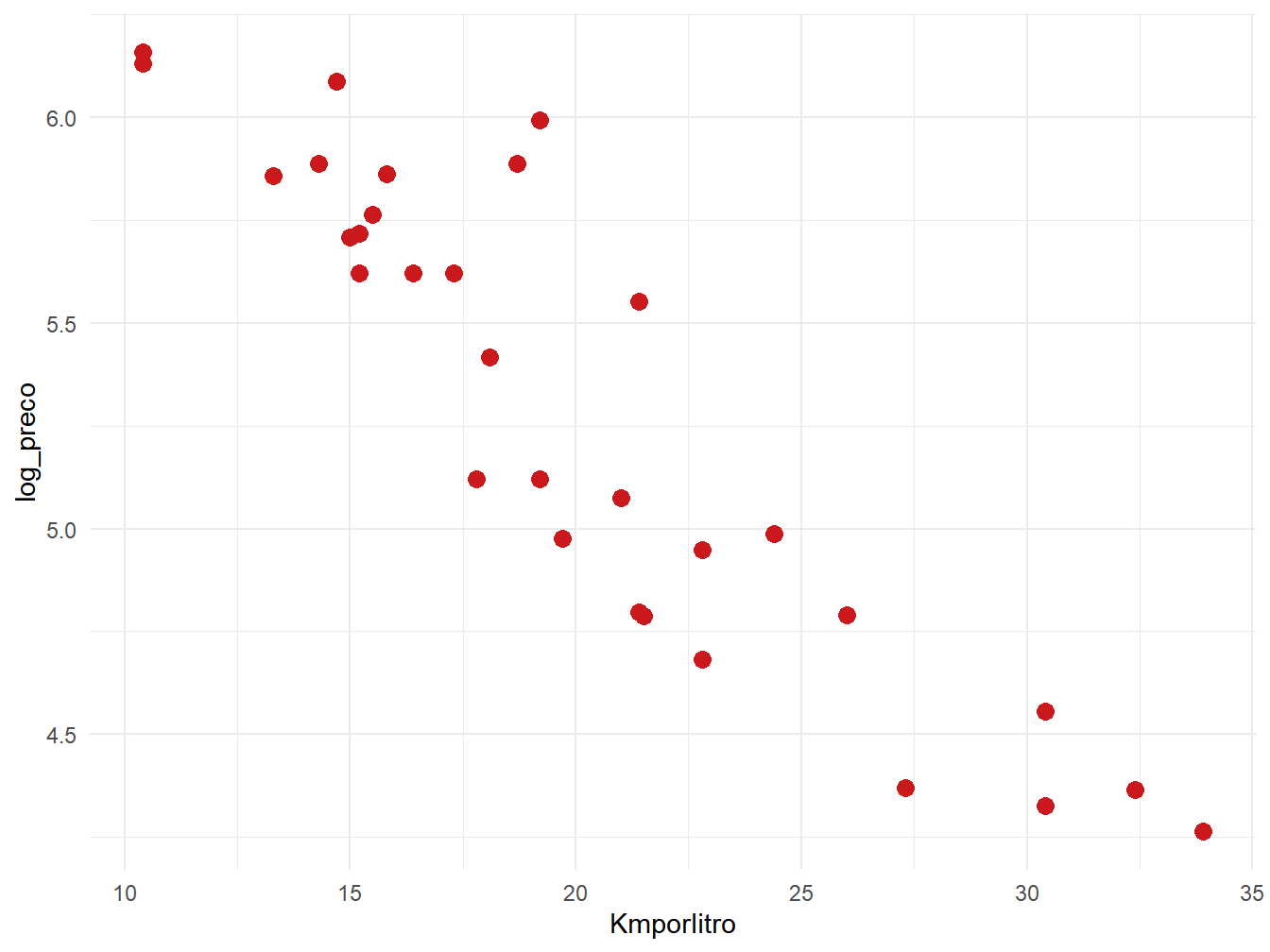
Figura 13.1: Diagrama de dispersão
##
## Pearson's product-moment correlation
##
## data: CARROS$log_preco and CARROS$Kmporlitro
## t = -11.805, df = 30, p-value = 0.00000000000084
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.9540391 -0.8167641
## sample estimates:
## cor
## -0.907111913.2 Teste de correlação de spearman
O Teste de correlação de spearman também faz a mensuração da associação linear entre duas variáveis quantitativas. Todavia, neste teste, as variaveis devem ser no mínimo do tipo ordinal.
13.2.0.1 Dados apropriados
Utiliza-se este teste quando:
* Os dados não seguem uma distribuição normal bi-variada.
13.2.0.2 Hipóteses
Hipótese nula: Não há associação [monotônica] entre as duas variáveis.
Hipótese alternativa: Há associação [monotônica] entre as duas variáveis.
13.2.0.3 Interpretação
Resultados significativos podem ser relatados como “Há associação entre as duas variáveis”.
13.2.0.4 Exemplo do teste de correlação
Este exemplo apresenta os dados de uma amostra de 32 carros.
Esse teste responde à pergunta: “A variável HP (quantitativa) é correlacionada com o preço (quantitativa)”
#-------------------------------------------------------------
### Banco de dados
data(mtcars)
CARROS<-mtcars
colnames(CARROS) <- c("Kmporlitro","Cilindros","Preco","HP",
"Amperagem_circ_eletrico","Peso","RPM",
"Tipodecombustivel","TipodeMarcha",
"NumdeMarchas","NumdeValvulas")
### Verifique os dados
str(CARROS$HP)## num [1:32] 110 110 93 110 175 105 245 62 95 123 ...## num [1:32] 160 160 108 258 360 ...### Remova objetos desnecessários
remove(mtcars)
#### Resumo dos dados
library(ggplot2)
ggplot(CARROS) +
aes(x = HP, y = Preco) +
geom_point(size = 3L, colour = "darkblue") +
theme_minimal()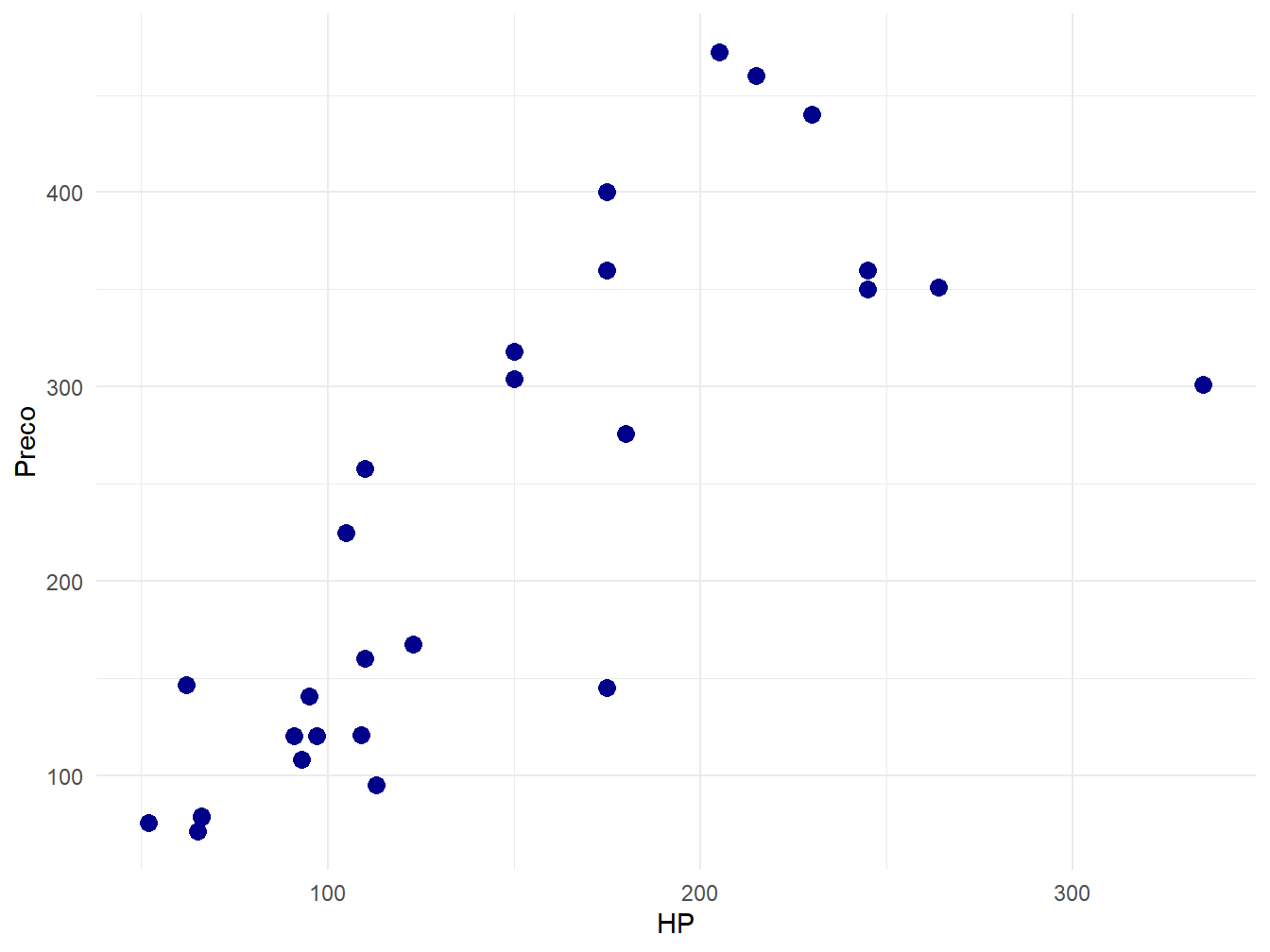
Figura 13.2: Diagrama de dispersão
##
## Spearman's rank correlation rho
##
## data: CARROS$HP and CARROS$Preco
## S = 812.71, p-value = 0.0000000006791
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.8510426Em breve vamos ter um módulo 2 contendo:
1. Regressão simples e multipla
2. Diagnostico em modelos de regressão
3. Modelos lineares Generalizados
Por enquanto, sugiro olhar as apresentações: