Capítulo 5 Testes de Hipóteses

Tradicionalmente, em um curso de Estatística há uma grande ênfase no teste de hipóteses e na tomada de decisões com base em p-valor. O teste de hipóteses é importante para determinar se há efeitos estatisticamente significativos.

5.0.0.1 Inferência estatística

A maior parte do que abordei até agora é sobre a produção de estatísticas descritivas: cálculo de médias, medianas, variância e desvio-padrão. Agora vamos abordar a inferência estatística: usando testes estatísticos para tirar alguma conclusão sobre os dados.

É natural para a maioria de nós utilizar astatísticas resumidas ou os gráficos, mas pular para a inferência estatística exige uma pequena mudança de perspectiva. A idéia de usar algum teste estatístico para responder a uma pergunta não é um conceito difícil, mas as próximas discussões ficarão um pouco teóricas.

Esse vídeo (em inglês) do Centro de Aprendizagem de Estatística explica bem a inferência estatística https://www.youtube.com/watch?v=tFRXsngz4UQ&list=PLp485I5glNfhYX6wTDB3wllRTtSJas_md

O teste de hipóteses é um procedimento estatístico que nos permite rejeitar ou não rejeitar uma hipótese através da evidência fornecida pela amostra. Em outras palavras, trata-se de uma metodologia estatística que nos auxilia a tomar decisões sobre uma ou mais populações, baseada na informação obtida da amostra.

5.0.0.2 Hipóteses Estatísticas

Uma suposição ou afirmação sobre parâmetros populacionais em forma numérica é chamada de hipótese estatística.

O Prof. Andre Zibetti afirma aqui que o tomar decisões, é comum a formulação de suposições ou de conjeturas sobre as populações de interesse, que, em geral, consistem em considerações sobre parâmetros (\[\mu, \sigma2\]) das mesmas. Essas suposições, que podem ser ou não verdadeiras, são denominadas de Hipóteses. Em muitas situações práticas, o interesse do pesquisador é verificar a veracidade sobre um ou mais parâmetros populacionais (\[\mu, \sigma2\]). Acredito que essa seja uma ótima definição.

5.0.0.3 Testando hipóteses

5.0.0.3.0.1 As hipóteses nulas e alternativas

Os métodos estatísticos contam com o teste de uma hipótese nula, que possui uma formulação específica para cada teste. A hipótese nula sempre descreve o caso em que, por exemplo, dois grupos não são diferentes ou não há correlação entre duas variáveis, etc. A hipótese alternativa é contrária à hipótese nula e, portanto, descreve os casos em que há uma diferença entre grupos ou há uma correlação entre duas variáveis, etc.

Observe que as definições de hipótese nula e hipótese alternativa não têm nada a ver com o que você deseja encontrar ou não, ou o que é interessante ou não. Se você estivesse comparando a altura de homens e mulheres, a hipótese nula seria que a altura dos homens e a altura das mulheres não fossem diferentes.

Da mesma forma, se você estivesse estudando a renda de homens e mulheres, a hipótese nula seria que a renda de homens e mulheres não é diferente na população que você está estudando. Nesse caso, você pode estar esperando que a hipótese nula seja verdadeira, embora não fique surpreso se a hipótese alternativa for verdadeira. De qualquer forma, a hipótese nula assumirá a forma de que não há diferença entre grupos, não há correlação entre duas variáveis ou não há efeito dessa variável em nosso modelo.

5.0.0.4 Definição de p-valor

A maioria dos testes de hipóteses se baseia no uso do p-valor para avaliar se devemos rejeitar ou deixar de rejeitar a hipótese nula. Dado que a hipótese nula é verdadeira, o p-valor é definido como a probabilidade de obter um resultado igual ou mais extremo do que o que foi realmente observado nos dados.

5.0.0.5 Regra de decisão

O p-valor para os dados fornecidos será determinado pela realização do teste estatístico.

Este p-valor é então comparado com um valor de alpha pré-determinado. Geralmente, um valor alpha de 0,05 é usado, mas não há nada de mágico nesse valor. Dependendo do seu estudo, você pode usar 0,01 ou 0,1 como valor de alpha.

Se o p-valor para o teste for menor que alpha, rejeitamos a hipótese nula. Se o p-valor for maior ou igual a alpha, falhamos em rejeitar a hipótese nula.

5.0.0.6 Exemplo de lançamento de moeda

Para um exemplo do uso do p-valor para o teste de hipóteses, imagine que você tenha uma moeda que jogará 100 vezes.

A hipótese nula é que a moeda é justa - isto é, que é igualmente provável que a moeda caia sobre as faces cara/coroas. Temos 50% para cada face da moeda.

A hipótese alternativa é que a moeda não é justa. Digamos que, para esse experimento, você jogue a moeda 100 vezes e ela dê cara 94 vezes. O p-valor nesse caso seria a probabilidade de obter 94, 95, 96, 97, 98, 99 ou 100 caras, assumindo que a hipótese nula seja verdadeira (moeda honesta).

Usando a notação matemática:

\[H0: p = 0,5 \ (hipótese \ nula)\] \[H1: p \neq 0,5 \ (hipótese\ alternativa)\]

Você pode imaginar que o p-valor para esses dados será bem pequeno. Se a hipótese nula for verdadeira e a moeda for justa, haveria uma baixa probabilidade de obter 94 ou mais caras (ou 94 ou mais coroas).

Usando um teste binomial, o valor-p é < 0,0000001. (Na verdade, R o informa como <2.2e-16, que é uma abreviação para o número na notação científica, 2,2 x 10-16, que é 0,00000000000000022, com 15 zeros após o ponto decimal)

Considerando um alpha de 0,05, uma vez que o p-valor é menor que alpha, rejeitamos a hipótese nula. Ou seja, concluímos que a moeda não é honesta.

binom.test(94, 100, 0.5)

## 
##  Exact binomial test
## 
## data:  94 and 100
## number of successes = 94, number of trials = 100, p-value <
## 0.00000000000000022
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.8739701 0.9776651
## sample estimates:
## probability of success 
##                   0.94

Como o p-valor é menor que 0,05, vamos concluir que é improvável que uma moeda honesta gere 94 caras. Em outras palavras, vamos concluir que p != 0,5 (a moeda é desonesta).

5.0.0.7 Lançamento de outra moeda

Agora imagine que você queira testar se uma outra moeda é honesta. Assim, vamos jogá-la 1.000 vezes. O resultado foi 540 caras. Com essas informações, decida se a moeda é honesta ou não.

• A pergunta é: uma moeda honesta pode gerar 540 caras em 1.000 lançamentos? Vamos ver o gráfico.

library(ggplot2)
library(grid)

x1  <- 450:550
df <- data.frame(x = x1, y = dbinom(x1, 1000, 0.5))

ggplot(df, aes(x = x, y = y)) + 
  geom_bar(stat = "identity", col = "#008080", fill = "#008080") + 
  scale_y_continuous(expand = c(0.01, 0)) + 
  xlab("Número de Caras") + ylab("Densidade") + 
  labs(title = "Número de Caras em 1.000 lançamentos de uma moeda") + 
  theme_bw(16, "serif") + 
  theme(plot.title = element_text(size = rel(1.2), vjust = 1.5))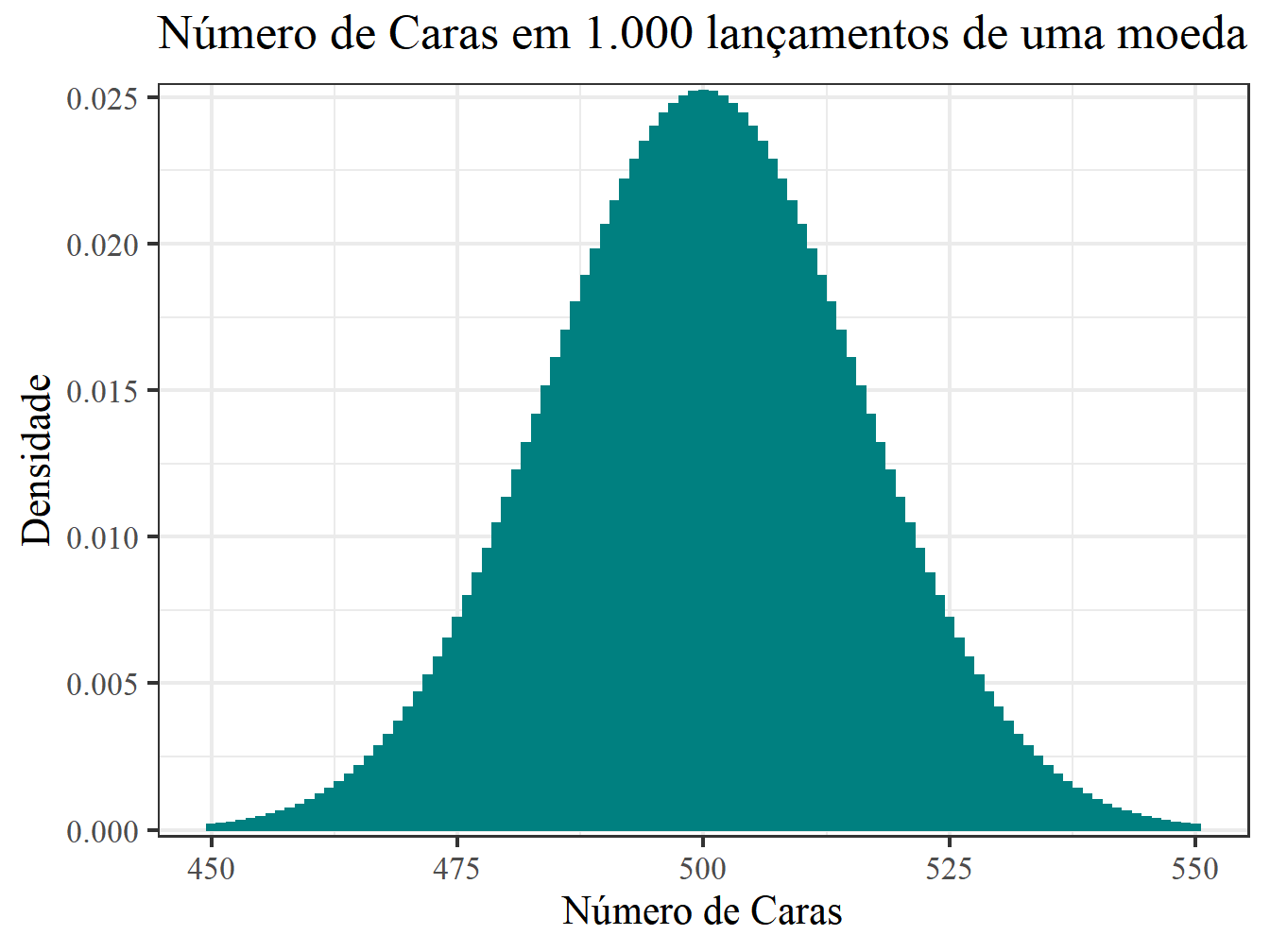

Figura 5.1: lançamento

Em uma análise gráfica, parece improvável que uma moeda honesta gere 540 caras. Para ter certeza, vamos realizar o teste.

Primeiro passo: formular as hipóteses.

\[H0: p = 0,5 \ (hipótese \ nula)\]

\[H1: p \neq 0,5 \ (hipótese\ alternativa)\]

Segundo passo: Criar uma regra de decisão.

Se p-valor < 0,05 rejeito H0

Terceiro passo: Realizar o teste

binom.test(540, 1000, 0.5)

## 
##  Exact binomial test
## 
## data:  540 and 1000
## number of successes = 540, number of trials = 1000, p-value = 0.01244
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.5085302 0.5712337
## sample estimates:
## probability of success 
##                   0.54

Quarto passo: Concluir a partir do resultado

• p-valor = 0,01244
  
• alpha = 0,05

Como p-valor < 0,05,** Rejeito H0 **. Ou seja, “Essa moeda também não é honesta”

5.0.0.8 Espere, isso faz algum sentido?

Lembre-se de que a definição do p-valor é: Dado que a hipótese nula é verdadeira, o p-valor é definido como a probabilidade de obter um resultado igual ou mais extremo do que o que foi realmente observado nos dados.

Na prática, usamos os resultados dos testes estatísticos para chegar a conclusões sobre a hipótese nula. Tecnicamente, o p-valor não diz nada sobre a hipótese alternativa. Mas logicamente, se a hipótese nula é rejeitada, seu complemento lógico, a hipótese alternativa, é apoiado.

5.0.0.9 Estatística é como um júri

Observe o discurso utilizado ao testar a hipótese nula. Com base nos resultados de nossos testes estatísticos, rejeitamos a hipótese nula ou deixamos de rejeitar a hipótese nula.

Isso é um semelhante à abordagem de um júri em um julgamento. O júri encontra evidências suficientes para declarar alguém culpado ou falha em encontrar evidências suficientes para declarar alguém culpado. Ou ele é culpado ou não-culpado (guilty or not guilty).

Não-culpado é diferente de inocente. A sentença de absolvição do juri não é um certificado de inocência. Varias coisas podem acontecer: 1) o promotor não fez o trabalho direito, 2) a pessoa é inocente, 3) o policial contaminou a cena do crime, etc… Ou temos evidências sobre a culpa e ele é condenado ou alguma coisa aconteceu.

Não condenar alguém não é necessariamente o mesmo que declarar alguém inocente. Da mesma forma, se não conseguirmos rejeitar a hipótese nula, não devemos assumir que a hipótese nula é verdadeira. Pode ser que não tenhamos amostras suficientes para obter um resultado que nos permita rejeitar a hipótese nula, ou talvez haja alguns outros fatores que afetam os resultados pelos quais não consideramos. Isso é semelhante a uma postura de “inocente até que se prove o contrário”.

IMPORTANTE

Por esse motivo, NUNCA use o termo aceitar a hipótese nula. Ou rejeitamos H0 ou não rejeitamos H0. Não rejeitar H0 é diferente de aceitar H0.

5.0.0.10 Erros do tipo 1 e tipo 2

Na maioria das vezes, os testes estatísticos que são utilizados são baseados em probabilidade, e os nossos dados sempre podem ser o resultado do acaso. Considerando o exemplo de lançamento de moeda acima, se jogássemos uma moeda 100 vezes e tivéssemos 94 caras, seríamos obrigados a concluir que a moeda não era justa. Mas 94 caras poderiam acontecer com uma moeda justa estritamente por acaso.

Podemos cometer dois tipos de erros ao testar a hipótese nula:

• Um erro do tipo I ocorre quando a hipótese nula é verdadeira, mas com base em nossa regra de decisão, rejeitamos a hipótese nula. Nesse caso, nosso resultado é um falso positivo; achamos que há um efeito (moeda injusta, associação entre variáveis, diferença entre grupos) quando realmente não existe. A probabilidade de cometer esse erro de tipo é alpha, o mesmo alpha que usamos em nossa regra de decisão.
• Um erro do tipo II ocorre quando a hipótese nula é falsa, mas com base em nossa regra de decisão, falhamos em rejeitar a hipótese nula. Nesse caso, nosso resultado é um falso negativo; falhamos em encontrar um efeito que realmente existe. A probabilidade de cometer esse tipo de erro é chamada beta.

A tabela a seguir resume esses erros. *inserir a tabela

5.0.0.10.1 Uma metáfora: Teste de hipóteses é como um julgamento

Imagine que você tenha dois professores (um carrasco e um mamata). Agora imagine que carrasco é tão rigoroso que acaba reprovando o melhor aluno da turma. Já o prof. mamata acabou de aprovar um dos piores da classe. O que é pior? Reprovar um estudante que sabe a materia ou aprovar um aluno que não sabe nada?

Procedimento parecido acontece nos testes de hipóteses. Se você aumentar muito o rigor do teste de hipóteses (alpha), somente evidências extraordinárias rejeitaria a hipótese nula. Se você aumentar a tolerância ao erro associado ao alpha e diminuir o erro relacionado ao beta, rejeitaria facilmente a hipótese nula mesmo quando há pouca evidência (na terminologia estatística, chamamos isso de tamanho do efeito).

Gostaria do seu feedback. Essa metáfora faz sentido?

5.0.0.11 Boas práticas para análises estatísticas

Ao analisar os dados, o analista não deve abordar a tarefa como faria um advogado da acusação. Ou seja, o analista não deve procurar efeitos e testes significativos, mas deve ser como um investigador independente, usando evidência para descobrir o que é mais provável de ser verdade.

5.0.0.12 O que é p-hacking?

Este seguimento é uma tradução de (Mangiafico 2015)

É importante, ao abordar testes de hipóteses do seu banco de dados, evitar cometer p-hacking do p-valor.

Imagine o caso em que o pesquisador coleta muitas medidas diferentes em uma variedade de assuntos. O pesquisador pode ficar tentado a simplesmente fazer muitos testes e modelos diferentes para relacionar uma variável a outra, mas para todas as variáveis. Ele pode continuar fazendo isso até encontrar um teste com um p-valor significativo. Isso seria uma forma de fazer o p-hacking.

Como um valor alfa de 0,05 nos permite cometer um erro falso positivo cinco por cento do tempo, encontrar um p-valor abaixo de 0,05 após vários testes sucessivos pode ser simplesmente devido ao acaso. Algumas formas de hackers com p-valor são mais flagrantes. Por exemplo, se alguém coletar alguns dados, execute um teste e continue a coletar dados e execute os testes iterativamente até encontrar um p-valor significativo.

5.0.0.12.0.1 Consequência do p-hacking: Viés de publicação

Este seguimento é uma tradução de (Mangiafico 2015)

Uma questão relacionada à ciência é que existe um viés para publicar ou relatar apenas os resultados significativos. Isso também pode levar a uma inflação da taxa de falsos positivos.

Como um exemplo hipotético, imagine se atualmente há 20 estudos semelhantes sendo testados com um efeito semelhante - digamos o efeito dos suplementos de glucosamina na dor nas articulações.

Se 19 desses estudos não encontraram efeito e foram descartados, mas um estudo encontrou um efeito usando um alfa de 0,05 e foi publicado, isso é realmente algum suporte para que os suplementos de glucosamina diminuam a dor nas articulações?

5.0.0.13 Discussão opcional: métodos alternativos ao teste de hipóteses

A controvérsia do teste de hipóteses. Particularmente nos campos da psicologia e da educação, tem havido muitas críticas à abordagem do teste de hipóteses. Na minha leitura, as principais queixas contra o teste de hipóteses tendem a ser:

• Geralmente, usamos um alpha de 0,05 como um ponto de corte mágico. Não faz muito sentido chegar a uma conclusão se nosso p-valor 0,049 e a conclusão oposta se nosso p-valor for 0,051.
• O p-valor está desatualizado e não faz sentido com big data: tudo se torna estatisticamente significativo.
• Alunos e pesquisadores realmente não entendem o significado do p-valor.
• P-hacking

Qual abordagem podemos utilizar conjugado com o teste de hipóteses para mitigar esses problemas? Deixo essa pergunta para você. Pessoalmente temos dois métodos promissores. 1 - Método Bayesiano, 2 - Machine Learning

Essas críticas foram retiradas dos textos a seguir:

A Dirty Dozen: Twelve P-Value Misconceptions

Testing for Publication Bias in Political Science

The p-Value You Can’t Buy

Misconceptions, Misuses, and Misinterpretations of P Values and Significance Testing

Show Me the Magnitude! The Consequences of Overemphasis on Null Hypothesis Significance Testing

The Enduring Evolution of the P Value


Em breve vou desenvolver o restante do conteúdo sobre testes de hipóteses. Nesse momento sugiro ver os livros do (Bussab and Morettin 2015) e (Agresti and Finlay 2012).

Referências

Agresti, Alan, and Barbara Finlay. 2012. Métodos Estatísticos Para as Ciências Sociais. Editora Penso. https://www.grupoa.com.br/.

Bussab, Wilton, and Pedro Morettin. 2015. Estatística Básica. Editora Saraiva. https://www.editorasaraiva.com.br.

Mangiafico, S. S. 2015. An R Companion for the Handbook of Biological Statistics, Version 1.3.2. https://rcompanion.org/rcompanion/.